
如图,OM⊥ON.已知边长为2的正三角形 ,两顶点
,两顶点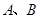 分别射线OM,ON上滑动,当∠OAB = 21°时, ∠NBC = 。滑动过程中,连结OC,则OC的长的最大值是 。
分别射线OM,ON上滑动,当∠OAB = 21°时, ∠NBC = 。滑动过程中,连结OC,则OC的长的最大值是 。
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
| 5 |
| 5 |

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC;
如图所示已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC;查看答案和解析>>
科目:初中数学 来源:2012-2013学年浙江杭州亭趾实验学校八年级上期中考试数学试题(解析版) 题型:填空题
如图,OM⊥ON.已知边长为2的正三角形 ,两顶点
,两顶点 分别射线OM,ON上滑动,当∠OAB = 21°时, ∠NBC
= 。滑动过程中,连结OC,则OC的长的最大值是
。
分别射线OM,ON上滑动,当∠OAB = 21°时, ∠NBC
= 。滑动过程中,连结OC,则OC的长的最大值是
。

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,OM⊥ON.已知边长为4的正三角形![]() ,两顶点
,两顶点![]() 分别射线OM,ON上滑动,当∠OAB = 31°时, ∠NBC = 。滑动过程中,连结OC,则OC的长的最大值是 .
分别射线OM,ON上滑动,当∠OAB = 31°时, ∠NBC = 。滑动过程中,连结OC,则OC的长的最大值是 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com