
����Ŀ���������ϵĵ�P�������²������Ȱѵ�P��ʾ��������![]() ���ٰ���������Ӧ�ĵ�����ƽ��1����λ���õ���P�Ķ�Ӧ��P������A��B�������ϣ����߶�AB�ϵ�ÿ�����������������õ��߶�A��B�������е�A��B�Ķ�Ӧ��ֱ�ΪA����B������ͼ������A��ʾ�����ǩ�3�����A����ʾ������__������B����ʾ������2�����B��ʾ������__����֪�߶�AB�ϵĵ�E��������������õ��Ķ�Ӧ��E�����E�غϣ����E��ʾ������__��
���ٰ���������Ӧ�ĵ�����ƽ��1����λ���õ���P�Ķ�Ӧ��P������A��B�������ϣ����߶�AB�ϵ�ÿ�����������������õ��߶�A��B�������е�A��B�Ķ�Ӧ��ֱ�ΪA����B������ͼ������A��ʾ�����ǩ�3�����A����ʾ������__������B����ʾ������2�����B��ʾ������__����֪�߶�AB�ϵĵ�E��������������õ��Ķ�Ӧ��E�����E�غϣ����E��ʾ������__��
![]()

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ϵ�У�����ABCO�ı�OA��x���ϣ���OC��y���ϣ���B������Ϊ��1��3�����������ضԽ���AC���ۣ�B������D���λ�ã���AD��y���ڵ�E����ô��D������Ϊ�� �� 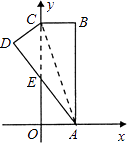
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
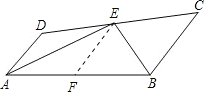
����Ŀ����ͼ��E���߶�CD�ϣ�EA��EB�ֱ�ƽ�֡�DAB�͡�CBA����AEB=90�㣬��AD=![]() ��BC=
��BC=![]() ����
����![]() ��
��
��1����AD��BC�ij���
��2������ΪAD��BC����ʲô��ϵ������֤��Ľ��ۣ�
��3��ȡAB�е�F������EF,��EF��AD��BC����EF=![]() ���������AB�ij��������ܣ���д���������̣������ܣ���˵�����ɣ�
���������AB�ij��������ܣ���д���������̣������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У����ǰѺᡢ�����궼�������ĵ�������㣬�ҹ涨���������ڲ� �������߽��ϵĵ㣮�۲���ͼ��ʾ��������ԭ�㡢һ��ƽ���� x ��������Σ��߳�Ϊ 1 ���������ڲ��� 1 �����㣬�߳�Ϊ 2 ���������ڲ��� 1 �����㣬�߳�Ϊ 3 ���������ڲ� �� 9 �����㣬������߳�Ϊ 10 ���������ڵ��������Ϊ�� ��

A. 64 �� B. 100 �� C. 81 �� D. 121 ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
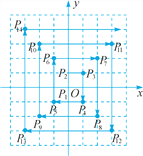
����Ŀ����ͼ����ƽ��ֱ������ϵ����ÿ����С����ı߳���Ϊ1����λ��P1��P2��P3�������ڸ��������˳��ͼ�������������������磺��P1(0��0)��P2(0��1)��P3(1��1)��P4(1����1)��P5(��1����1)��P6(��1��2)����.����������������P2018��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ��ȤС���о��ҹ��Ŵ����㷨ͳ�ڡ�������һ��ʫ�����ʿ������������ڿͶ��������У�һ���߿Ͷ��߿ͣ�һ���ſ�һ���գ�ʫ�к��������˼�ǣ����ÿһ��ͷ�ס7�ˣ���ô��7������ס�����ÿһ��ͷ�ס9�ˣ���ô�Ϳճ�һ�䷿��
��1����õ��пͷ����ټ䣿���Ͷ����ˣ�
��2������������������ͷ����и��������������ӣ�ÿ��ͷ��շ�20Ǯ����ÿ��ͷ������ס4�ˣ�һ���Զ��ͷ�18�����ϣ���18�䣩�����Ѱ�8���Żݣ���ʫ�С��ڿ͡��ٴ�һ����ס��������ζ��������㣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ױƷ���ϰ嵽����ѡ��A��B����Ʒ�ƵĻ�ױƷ��������AƷ�ƵĻ�ױƷ5�ף�BƷ�ƵĻ�ױƷ6�ף���Ҫ950Ԫ��������AƷ�ƵĻ�ױƷ3�ף�BƷ�ƵĻ�ױƷ2�ף���Ҫ450Ԫ��
��1����A��B����Ʒ�ƵĻ�ױƷÿ���۷ֱ�Ϊ����Ԫ��
��2��������1��AƷ�ƵĻ�ױƷ�ɻ���30Ԫ������1��BƷ�ƵĻ�ױƷ�ɻ���20Ԫ�������г�����ױƷ���ϰ����������BƷ�ƻ�ױƷ�������ȹ���AƷ�ƻ�ױƷ������2������4�ף���BƷ�ƻ�ױƷ���ɹ���40�ף�������ױƷȫ���۳���ʹ�ܵĻ���������1200Ԫ���ʣ����ļ��ֽ�����������ν�����ʹ�ɱ���ʡ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У�E��BC���е㣬����AE���ӳ���DC���ӳ����ڵ�F��

��1����֤��AB=CF��
��2������DE����AD=2AB����֤��DE��AF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���ABC��A��B����������x���ϣ�����C��y��ĸ������ϣ���֪|OA|��|OB|=1��5��|OB|=|OC|����ABC�����S��ABC=15��������y=ax2+bx+c��a��0������A��B��C���㣮
��1����������ߵĺ�������ʽ��
��2����E��y���Ҳ������������ڵ�B��һ�����㣬����E��x���ƽ���߽�����������һ��F������F��FG��ֱ��x���ڵ�G���ٹ���E��EH��ֱ��x���ڵ�H���õ�����EFGH�����ڵ�E���˶������У�������EFGHΪ������ʱ������������εı߳���
��3�������������Ƿ��������B��C�ĵ�M��ʹ��MBC��BC���ϵĸ�Ϊ ![]() �������ڣ������M�����ꣻ�������ڣ���˵�����ɣ�
�������ڣ������M�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com