
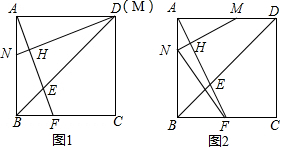
���� ��1�����������ε����ʵõ�AD=AB����BAD=90�㣬�ɴ�ֱ�Ķ���õ���AHM=90�㣬����ǵ����ʵõ���BAF=��AMH������ȫ�������ε����ʼ��ɵõ����ۣ�
��2���ٸ��ݹ��ɶ����õ�BD=6$\sqrt{2}$��������ã�DM=t��BE=$\sqrt{2}$t�����AM=6-t��DE=6$\sqrt{2}$-$\sqrt{2}$t���������������ε��ж������ʼ��ɵõ����ۣ�
�ڸ�����֪�����õ�AN=2��BN=4���������������ε����ʵõ�BF=$\frac{12}{6-t}$���ɢ����BF=$\frac{6t}{6-t}$���÷���$\frac{6t}{6-t}$=$\frac{12}{6-t}$�����ǵõ����ۣ�
��� �⣺��1�����ı���ABCD �������Σ�
��AD=AB����BAD=90�㣬
��MN��AF��
���AHM=90�㣬
���BAF+��MAH=��MAH+��AMH=90�㣬
���BAF=��AMH��
�ڡ�AMN���ABF�У�$\left\{\begin{array}{l}{��AMN=��BAF}\\{AM=AB}\\{��MAN=��BAF}\end{array}\right.$��
���AMN�ա�ABF��
��AF=MN��
��2���١�AB=AD=6��
��BD=6$\sqrt{2}$��
������ã�DM=t��BE=$\sqrt{2}$t��
��AM=6-t��DE=6$\sqrt{2}$-$\sqrt{2}$t��
��AD��BC��
���ADE�ס�FBE��
��$\frac{AD}{BF}=\frac{DE}{BE}$����$\frac{6}{y}=\frac{6\sqrt{2}-\sqrt{2}t}{\sqrt{2}t}$��
��y=$\frac{6t}{6-t}$��
�ڡ�BN=2AN��
��AN=2��BN=4��
�ɣ�1��֤�á�BAF=��AMN���ߡ�ABF=��MAN=90�㣬
���ABF�ס�AMN��
��$\frac{AM}{AB}$=$\frac{AN}{BF}$����$\frac{6-t}{6}$=$\frac{2}{BF}$��
��BF=$\frac{12}{6-t}$��
�ɢ����BF=$\frac{6t}{6-t}$��
��$\frac{6t}{6-t}$=$\frac{12}{6-t}$��
��t=2��
��BF=3��
��FN=$\sqrt{B{F}^{2}+B{N}^{2}}$=5cm��
���� ������Ҫ���������ε����ʺ����������Ρ�ȫ�������ε��ж������ʡ����ɶ�����֪ʶ����ۺ�Ӧ�ã�


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
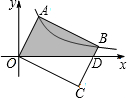
 ������L��y=a��x-x1����x-x2��������a��0����x�ύ�ڵ�A��x1��0����B��x2��0������y�ύ�ڵ�C����x1•x2��0��AB=4����ֱ��l��y=-3x+t+2������t��0��ͬʱ������A��Cʱ��t=1��
������L��y=a��x-x1����x-x2��������a��0����x�ύ�ڵ�A��x1��0����B��x2��0������y�ύ�ڵ�C����x1•x2��0��AB=4����ֱ��l��y=-3x+t+2������t��0��ͬʱ������A��Cʱ��t=1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
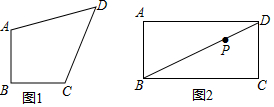
 ��ͼ����ֱ������ϵ�У�����OABC�Ķ���A��B��˫����y=$\frac{k}{x}$�� x��0���ϣ�BC��x�ύ�ڵ�D������A������Ϊ��2��4�������D������Ϊ��������
��ͼ����ֱ������ϵ�У�����OABC�Ķ���A��B��˫����y=$\frac{k}{x}$�� x��0���ϣ�BC��x�ύ�ڵ�D������A������Ϊ��2��4�������D������Ϊ��������| A�� | ��$\frac{22}{3}$��0�� | B�� | ��$\frac{15}{2}$��0�� | C�� | ��$\frac{68}{9}$��0�� | D�� | ��$\frac{48}{5}$��0�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����1��2��3��2��5�������3 | |
| B�� | ������ij����ÿ�춪�����ϴ������ĵ��飬Ӧ�����ղ�ķ�ʽ | |
| C�� | ��ͬһ�������367��ѧ���У����������˵�������ͬһ�� | |
| D�� | ���������ݵķ�����0.15���������ݵķ�����0.21�����������ݱȼ��������ȶ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | 5 | C�� | 6 | D�� | 9 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com