
����Ŀ����ͼ1��������ƬABCD�ij�Ϊ2a����Ϊa�� Ϊ��Ҫ����Ƭ�ܴ���ֱ��Ϊ ![]() ��Բ�ף������Ƭ���д������涨��Ƭ��Բ���нӴ�ʱ��Ƭ���ܴ���Բ�ף���
��Բ�ף������Ƭ���д������涨��Ƭ��Բ���нӴ�ʱ��Ƭ���ܴ���Բ�ף��� 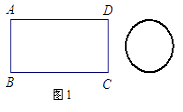
��1����ͼ2��M��N��P��Q�ֱ���AD��AB��BC��CD���е㣬����������Ƭ���ĸ���ȥ����ֻ�����ı���MNPQ�� �����ʱ��Ƭ��ʲô��״��
�ڸ���֤������ͨ������˵����ʱ��Ƭ���ܴ���Բ�ף�
��2����ͼ3����������ƬABCD��������һ��ֱ�߷ֱ�BC��AD�ڵ�E��F������˵��غϣ�����������ֱ�߽�������Ƭ�и������ȫ�ȵ�ֱ��������Ƭ�� 
�ٵ�BE=DF= ![]() ʱ���ж�ֱ��������ƬEBAF�ܷ�Բ�ף���˵�����ɣ�
ʱ���ж�ֱ��������ƬEBAF�ܷ�Բ�ף���˵�����ɣ�
��Ϊ����ʹֱ��������ƬEBAF˳������Բ�ף���ֱ��д���߶�BE�ij��ȵ�ȡֵ��Χ��
���𰸡�
��1��������
����ͼ������M��MG��NP�ڵ�G��
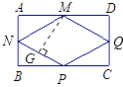
��M��N��P��Q�ֱ���AD��AB��BC��CD���е㣬
���AMN�ա�BPN�ա�CPQ�ա�DMQ��
��MN=NP=PQ=QM��
���ı���MNPQ�����Σ�
�� ![]() ��
��
MN= ![]() ��
��
��MG= ![]() ��
��
���ʱ��Ƭ�ܴ���Բ�ף�
��2������ͼ������A��AH��EF�ڵ�H������E��EK��AD�ڵ�K��
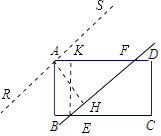
��ȻAB= ![]() ��
��
��������AB��ֱ�ķ���������Բ�ף�
����A��EF��ƽ����RS����ֻ�����ֱ��RS��EF֮��ľ��뼴�ɣ�
��BE=AK= ![]() ��EK=AB=a��AF=
��EK=AB=a��AF= ![]() ��
��
��KF= ![]() ��EF=
��EF= ![]() ��
��
�ߡ�AHF=��EKF=90�㣬��AFH=��EFK��
���AHF�ס�EKF��
�� ![]() ���ɵ�AH=
���ɵ�AH= ![]() ��
��
���ֱ��������Ƭ���ܴ���Բ�ף�
�� ![]() ��
�� ![]() ��
��
����������1��������������ȵ��ı���Ϊ�������ж��ı���Ϊ���Σ�Ȼ���������������������һ�ߵĸߣ�����֪���ݱȽϺ��ж��Ƿ���ͨ������2�����������������Ƶõ������߶Σ����������A��EF�ľ��룬Ȼ������֪�߶αȽϣ��Ӷ��ж��ܷ�ͨ����
�����㾫����������Ĺؼ���������ֱ����Բ������λ�ù�ϵ�����֪ʶ������ֱ����Բ������λ�ù�ϵ��������Ϊ���룻������������Ϊ�ཻ,����ֱ�߽���Բ�ĸ��ߣ�Բ��ֱ����Ψһ������Ϊ���У�����ֱ�߽���Բ�����ߣ����Ψһ�Ĺ���������е㣬�Լ������������ε��ж������ʵ����⣬�˽����������ε�һ�ж�Ӧ�߶�(��Ӧ�ߡ���Ӧ���ߡ���Ӧ��ƽ���ߡ����Բ�뾶������Բ�뾶�ȣ��ıȵ������Ʊȣ������������ܳ��ıȵ������Ʊȣ���������������ıȵ������Ʊȵ�ƽ����


 ��ҵ����ϵ�д�
��ҵ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������̼�����ѽ�����Ϊ���ǵ�ϰ�ߣ������Ϊ�س��������˹���������ֻ��Ҫ����Ѻ�𣬾Ϳ���ͨ��ɨ���ά��ķ�ʽ����һ��ͣ��·�ߵ����г����Լ��͵ķ��ã������ﵽĿ�ĵأ�����ʦ����ѧУ���2km������ÿ���ﹲ��������ѧУ������ʱ��ȹ�ȥ��綯������4min����֪����ʦ��綯�����ٶ����ﹲ�������ٶȵ�1.5����������ʦ�ﹲ���������ٶ��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
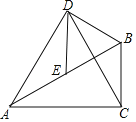
����Ŀ����ͼ����Rt��ABC�У���M2��N2������BAC=30�㣬EΪAB�ߵ��е㣬��BEΪ�����ȱ���BDE������AD��CD��
��1����֤����ADE�ա�CDB��
��2����BC=![]() ����AC������һ��H��ʹ��BH+EH��С������������Сֵ��
����AC������һ��H��ʹ��BH+EH��С������������Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���A=64�㣬��ABC���ACD��ƽ���߽��ڵ�A1 �� ���A1=����A1BC���A1CD��ƽ�����ཻ�ڵ�A2 �� �á�A2��������An��1BC���An��1CD��ƽ�����ཻ�ڵ�An �� Ҫʹ��An�Ķ���Ϊ��������n��ֵ���Ϊ �� 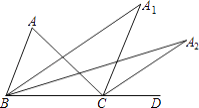
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���϶��ĺ�̽������2019��1��3�գ��ɹ���½�������棬ͨ����ȵ�����м��Ǵ����������һ�Ž�����������±�Ӱ��ͼ����������������̽����ƪ�£����м��dzɹ������ڵ�����������L2��ʱ�����������Լ1500000km���ÿ�ѧ��������ʾ��1500000Ϊ( )

A. 15��105 B. 1.5��106 C. 0.15��107 D. 1.5��105
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��������OABC�ı�OA�������ϣ�OΪԭ�㣬������OABC�����Ϊ12��OC�߳�Ϊ3.

(1)�����ϵ�A��ʾ����Ϊ________��
(2)��������OABC������ˮƽ�ƶ����ƶ���ij����μ�ΪO��A��B��C�����ƶ���ij�����O��A��B��C����ԭ������OABC�ص�����(��ͼ2����Ӱ����)�������ΪS.
�ٵ�Sǡ�õ���ԭ������OABC�����һ��ʱ�������ϵ�A����ʾ�����Ƕ��٣�
�� �����A���ƶ�����AA����x.
�� ����)��S��4ʱ����x��ֵ��
�� ����)DΪ�߶�AA�����е㣬��E���߶�OO���ϣ���OE��![]() OO��������D��E����ʾ������Ϊ�෴��ʱ����x��ֵ��
OO��������D��E����ʾ������Ϊ�෴��ʱ����x��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
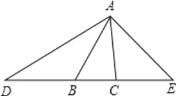
����Ŀ����ͼ���ڡ�ABC �У���ABC��50�㣬��ACB��80�㣬�ӳ� CB �� D��ʹ DB��BA���ӳ� BC �� E��ʹ CE��CA������ AD �� AE�����D����DAE �Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
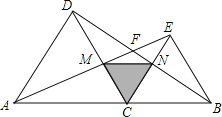
����Ŀ����ͼ����C���߶�AB�ϳ�A��B�������һ�㣬�ֱ���AC��BCΪ�����߶�AB��ͬ�����ȱ�������ACD�͵ȱ�������BEC������AE��DC��M������BD��CE��N��AE��BD����F
��1����֤��AE=BD��
��2������MN����ϸ�۲���MNC����״��������MNC��ʲô�����Σ�˵����IJ��룬������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺
(1)|��2|��(��![]() )��(��5)��(��2); (2)(
)��(��5)��(��2); (2)(![]() ��
��![]() ��
��![]() )��(��24)��
)��(��24)��
(3)15��(��![]() ��
��![]() ); (4)(��2)2��|��7|��3��(��
); (4)(��2)2��|��7|��3��(��![]() )��(��3)3��(��
)��(��3)3��(��![]() )2.
)2.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com