
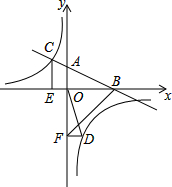
 如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数y=$\frac{k}{x}$(k≠0)的图象在第二象限交于点C,CE⊥x轴,垂足为点E,sin∠ABO=$\frac{\sqrt{5}}{5}$,OB=2,OE=1.
如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数y=$\frac{k}{x}$(k≠0)的图象在第二象限交于点C,CE⊥x轴,垂足为点E,sin∠ABO=$\frac{\sqrt{5}}{5}$,OB=2,OE=1.分析 (1)由边的关系可得出BE=6,通过解直角三角形可得出CE=3,结合函数图象即可得出点C的坐标,再根据点C的坐标利用反比例函数图象上点的坐标特征,即可求出反比例函数系数m,由此即可得出结论;
(2)由点D在反比例函数在第四象限的图象上,设出点D的坐标为(n,-$\frac{3}{2n}$)(n>0).通过解直角三角形求出线段OA的长度,再利用三角形的面积公式利用含n的代数式表示出S△BAF,根据点D在反比例函数图形上利用反比例函数系数k的几何意义即可得出S△DFO的值,结合题意给出的两三角形的面积间的关系即可得出关于n的分式方程,解方程,即可得出n值,从而得出点D的坐标.
解答 解:(1)∵OB=2,OE=1,
∴BE=OB+OE=3.
∵CE⊥x轴,
∴∠CEB=90°.
在Rt△BEC中,∠CEB=90°,BE=3,sin∠ABO=$\frac{\sqrt{5}}{5}$,
∴tan∠ABO=$\frac{1}{2}$,
∴CE=BE•tan∠ABO=3×$\frac{1}{2}$=$\frac{3}{2}$,
结合函数图象可知点C的坐标为(-1,$\frac{3}{2}$).
∵点C在反比例函数y=$\frac{k}{x}$的图象上,
∴k=-1×$\frac{3}{2}$=-$\frac{3}{2}$,
∴反比例函数的解析式为y=-$\frac{3}{2x}$.
(2)∵点D在反比例函数y=-$\frac{3}{2}$x第四象限的图象上,
∴设点D的坐标为(n,-$\frac{3}{2n}$)(n>0).
在Rt△AOB中,∠AOB=90°,OB=4,tan∠ABO=$\frac{1}{2}$,
∴OA=OB•tan∠ABO=2×$\frac{1}{2}$=1.
∵S△BAF=$\frac{1}{2}$AF•OB=$\frac{1}{2}$(OA+OF)•OB=$\frac{1}{2}$(1+$\frac{3}{2n}$)×2=1+$\frac{3}{2n}$.
∵点D在反比例函数y=-$\frac{3}{2n}$第四象限的图象上,
∴S△DFO=$\frac{1}{2}$×|-$\frac{3}{2}$|=$\frac{3}{4}$.
∵S△BAF=4S△DFO,
∴1+$\frac{3}{2n}$=4×$\frac{3}{2}$,
解得:n=$\frac{3}{10}$,
经验证,n=$\frac{3}{10}$是分式方程的解,∴点D的坐标为($\frac{3}{10}$,-2).
点评 本题考查了解直角三角形、反比例函数图象上点的坐标特征、三角形的面积公式以及反比例函数系数k的几何意义,解题的关键是:(1)求出点C的坐标;(2)根据三角形的面积间的关系找出关于n的分式方程.本题属于中档题,难度不大,但较繁琐,解决该题型题目时,找出点的坐标,再利用反比例函数图象上点的坐标特征求出反比例函数系数是关键.


科目:初中数学 来源: 题型:填空题
 如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,竹条AB的长为25cm,贴纸部分的宽BD为15cm,若纸扇两面贴纸,则一面贴纸的面积为175πcm2(结果保留π).
如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,竹条AB的长为25cm,贴纸部分的宽BD为15cm,若纸扇两面贴纸,则一面贴纸的面积为175πcm2(结果保留π).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
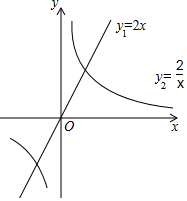 在平面直角坐标系xOy中,直线y1=2x与双曲线y2=$\frac{2}{x}$ 的图象如图所示,小明说:“满足y1>y2的x的取值范围是x>1.”你同意他的观点吗?答:不同意.理由是y1>y2的x的取值范围是x>1或-1<x<0.
在平面直角坐标系xOy中,直线y1=2x与双曲线y2=$\frac{2}{x}$ 的图象如图所示,小明说:“满足y1>y2的x的取值范围是x>1.”你同意他的观点吗?答:不同意.理由是y1>y2的x的取值范围是x>1或-1<x<0.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
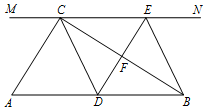 如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上
如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com