
【题目】在下列解题过程的空白处填上适当的内容(推理的理由或数学表达式)
如图,已知AB∥CD,BE、CF分别平分∠ABC和∠DCB,求证:BE∥CF.
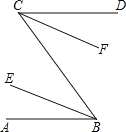
证明:
∵AB∥CD,(已知)
∴∠ =∠ .( )
∵ ,(已知)
∴∠EBC=![]() ∠ABC,(角的平分线定义)
∠ABC,(角的平分线定义)
同理,∠FCB= ![]() ∠BCD .
∠BCD .
∴∠EBC=∠FCB.(等式性质)
∴BE∥CF.( )
 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
【题目】南山植物园中现有A、B两个园区,已知A园区为长方形,长为(x+y)米,宽为(x﹣y)米;B园区为正方形,边长为(x+3y)米.
(1)请用代数式表示A、B两园区的面积之和并化简;
(2)现根据实际需要对A园区进行整改,长增加(11x﹣y)米,宽减少(x﹣2y)米,整改后A区的长比宽多350米,且整改后两园区的周长之和为980米.
①求x、y的值;
②若A园区全部种植C种花,B园区全部种植D种花,且C、D两种花投入的费用与吸引游客的收益如表:

求整改后A、B两园区旅游的净收益之和.(净收益=收益﹣投入)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索与运用:
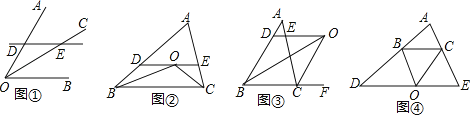
(1)基本图形:如图①,已知OC是∠AOB的角平分线,DE∥OB,分别交OA、OC于点D、E.求证:DE=OD;
(2)在图②中找出这样的基本图形,并利用(1)中的规律解决这个问题:已知△ABC中,两个内角∠ABC与∠ACB的平分线交于点O,过点O作DE∥BC,交AB、AC于点D、E.求证:DE=BD+CE;
(3)若将图②中两个内角的角平分线改为一个内角(如图③,∠ABC)、一个外角(∠ACF)和两个都是外角(如图④∠DBC、∠BCE)的角平分线,其它条件不变,则线段DE、BD、CE的数量关系分别是:图③为 、图④为 :并从中任选一个结论证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
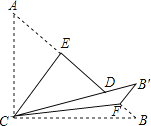
【题目】如图,Rt△ABC,∠ACB=90°,AC=3,BC=4,将边Ac沿CE翻折,使点A落在AB上的D处,再将边BC沿CF翻折,使点B落在CD的延长线上的点F处,两条折痕与斜边AB分别交于点E、F,则线段BF的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,P是∠ABC内一点,请过点P画射线PD,使PD∥BC;过点P画直线PE∥BA,交BC于点E.请画图并通过观察思考后你发现∠ABC与∠DPE的大小关系是 ,并说明理由.
(2)如图2,直线a,b所成的角跑到画板外面去了,为了测量这两条直线所成的角的度数,请画图并简单地写出你的方法.

查看答案和解析>>
科目:初中数学 来源: 题型:
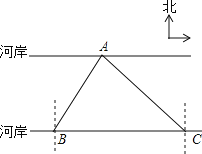
【题目】如图,要测量A点到河岸BC的距离,在B点测得A点在B点的北偏东30°方向上,在C点测得A点在C点的北偏西45°方向上,又测得BC=150m.求A点到河岸BC的距离.(结果保留整数)(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A和B两地相距140千米,甲、乙二人骑自行车分别从A和B两地同时出发,相向而行.丙驾驶摩托车,每小时行驶63千米,同时与甲从A出发,与乙相遇后立即返回,丙返回至甲时,甲、乙相距84千米.若甲车速是每小时9千米,则乙的速度为 千米/时.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com