
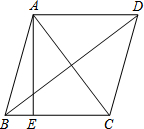
 已知菱形ABCD的两条对角线AC,BD长分别为6cm、8cm,且AE⊥BC,这个菱形的面积S=
已知菱形ABCD的两条对角线AC,BD长分别为6cm、8cm,且AE⊥BC,这个菱形的面积S= 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:初中数学 来源: 题型:
| 商品 价格 | A | B |
| 进价(元/件) | 1200 | 1000 |
| 售价(元/件) | 1350 | 1200 |
查看答案和解析>>
科目:初中数学 来源: 题型:
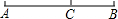 电视节目主持人在主持节目时,站在舞台的黄金分割点处最自然得体,如图,若舞台AB长20米,主持人站在C处恰好最自然得体,则AC长约为
电视节目主持人在主持节目时,站在舞台的黄金分割点处最自然得体,如图,若舞台AB长20米,主持人站在C处恰好最自然得体,则AC长约为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com