
分析 (1)方程利用平方根定义开方即可求出解;
(2)方程组整理后,利用加减消元法求出解即可.
解答 解:(1)方程开方得:2x-1=6或2x-1=-6,
解得:x1=3.5,x2=-2.5;
(2)方程组整理得:$\left\{\begin{array}{l}{21x+5y=104①}\\{14x-13y=4②}\end{array}\right.$,
①×2-②×3得:49y=196,即y=4,
把y=4代入①得:x=4,
则方程组的解为$\left\{\begin{array}{l}{x=4}\\{y=4}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
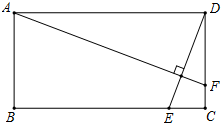 如图,矩形ABCD中,AB=2,AD=4,动点E在边BC上,与点B、C不重合,过点A作DE的垂线,交直线CD于点F.设DF=x,EC=y.
如图,矩形ABCD中,AB=2,AD=4,动点E在边BC上,与点B、C不重合,过点A作DE的垂线,交直线CD于点F.设DF=x,EC=y.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
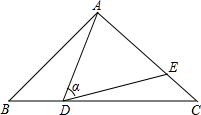 如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=$\frac{4}{5}$.下列结论:①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8;④0<CE≤6.4.其中正确的结论是①②④.(把你认为正确结论的序号都填上)
如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=$\frac{4}{5}$.下列结论:①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8;④0<CE≤6.4.其中正确的结论是①②④.(把你认为正确结论的序号都填上)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知线段a和b,a>b,求作直角三角形ABC,使直角三角形的斜边AB=a,直角边AC=b.(用尺规作图,保留作图痕迹,不要求写作法)
如图,已知线段a和b,a>b,求作直角三角形ABC,使直角三角形的斜边AB=a,直角边AC=b.(用尺规作图,保留作图痕迹,不要求写作法)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com