
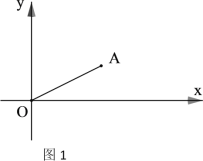
【题目】如图1,在平面直角坐标系中,已知A(a,b),且a.b满足![]() ,
,
(1)求A点的坐标及线段OA的长度;(2)点P为x轴正半轴上一点,且△AOP是等腰三角形,求P点的坐标;
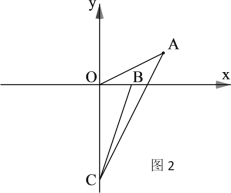
(3)如图2,若B(1,0),C(0,-3),试确定∠ACO+∠BCO的值是否发生变化,若不变,求其值;若变化,请求出变化范围。
【答案】(1)![]() ;(2)P(
;(2)P(![]() ,0)或P(4,0)、P(
,0)或P(4,0)、P(![]() ,0);(3)45.
,0);(3)45.
【解析】
(1)先由二次根式有意义的条件得出a的值,再代入等式得出b的值,从而得出点A的坐标,继而利用两点间的距离公式可得OA的长;
(2)分OA=OP、AO=AP、PO=PA三种情况,利用等腰三角形的性质逐一求解可得;
(3)在x轴负半轴上取一点,使得OD=OB=1,知点B与点D关于y轴对称,据此得∠BCO=∠DCO,根据两点间的距离公式知AD2=10,CD2=10,AC2=20,依据勾股定理逆定理判断出△ACD是等腰直角三角形,利用∠ACO+∠BCO=∠ACO+∠DCO=∠ACD可得答案.
解:
(1)∵![]() ,
,
∴a=2,
则b=1,
∴A(2,1),
则OA=![]() =
=![]() ;
;
(2)当OA=OP时,P(![]() ,0);
,0);
当AO=AP时,如图1,作AH⊥x轴于点H,
则OH=PH=2,
∴OP=4,
∴P(4,0);
当P′O=P′A时,设P′O=P′A=x,则P′H=2-x,

由AP′2=P′H2+AH2得(2-x)2+12=x2,
解得:x=![]() ,
,
∴P(![]() ,0).
,0).
(3)如图2,在x轴负半轴上取一点,使得OD=OB=1,

则点B与点D关于y轴对称,
∴∠BCO=∠DCO,
∵A(2,1),D(-1,0),C(0,-3),
∴AD2=32+12=10,CD2=12+32=10,AC2=22+42=20,
∴AD2+CD2=AC2,且AD=CD,
∴△ACD是等腰直角三角形,
则∠ACO+∠BCO=∠ACO+∠DCO=∠ACD=45°.


科目:初中数学 来源: 题型:
【题目】问题背景
在数学活动课上,张老师要求同学们拿两张大小不同的矩形纸片进行旋转变换探究活动.如图 1,在矩形纸片ABCD 和矩形纸片EFGH中,AB=1,AD=2,且FE>AD,FG>AB,点E 是 AD 的中点,矩形纸片 EFGH 以点E 为旋转中心进行逆时针旋转,在旋转过程中会产生怎样的数量关系,提出恰当的数学问题并加以解决.
解决问题
下面是三个学习小组提出的数学问题,请你解决这些问题.
(1)“奋进”小组提出的问题是:如图 1,当 EF 与 AB 相交于点 M,EH 与 BC 相交于点 N 时,求证:EM=EN.
(2)“雄鹰”小组提出的问题是:在(1)的条件下,当 AM=CN 时,AM 与 BM 有怎样的数量关系,请说明理由.
(3)“创新”小组提出的问题是:若矩形 EFGH 继续以点 E 为旋转中心进行逆时针旋转,当 ![]() 时,请你在图 2 中画出旋转后的示意图,并求出此时 EF 将边 BC 分成的两条线段的长度.
时,请你在图 2 中画出旋转后的示意图,并求出此时 EF 将边 BC 分成的两条线段的长度.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织学生到外地进行社会实践活动,共有680名学生参加,并携带300件行李.学校计划租用甲、乙两种型号的汽车共20辆.经了解,甲种汽车每辆最多能载40人和10件行李,乙种汽车每辆最多能载30人和20件行李.
(1)如何安排甲、乙两种汽车可一次性地将学生和行李全部运走?有哪几种方案?
(2)如果甲、乙两种汽车每辆的租车费用分别为2000元、1800元,请你选择最省钱的一种租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A城气象台测得台风中心在A城正西方向600km的B处,以每小时200km的速度向北偏东60°的BC方向移动,距台风中心500km的范围是受台风影响的区域
(1)A城是否受这次台风的影响?
(2)若A城受到这次台风的影响,那么A城遭受台风影响有多长时间?

查看答案和解析>>
科目:初中数学 来源: 题型:
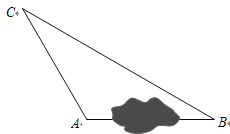
【题目】在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.现测得AC=50m,BC=100m,∠CAB=120°,请计算A,B两个凉亭之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
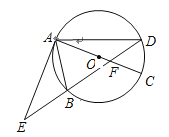
【题目】如图,⊙O的直径AC与弦BD相交于点F,点E是DB延长线上一点,∠EAB=∠ADB.
(1)求证:EA是⊙O的切线;
(2)已知点B是EF的中点,AF=4,CF=2,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校一班级开展为贫困山区学生捐钱助学活动,该班有20名学生捐出了自己的零花钱,捐款数如下:(单位:元)
19 | 20 | 25 | 30 | 28 | 27 | 26 | 21 | 20 | 22 | 24 | 23 | 25 | 29 | 27 | 28 | 27 | 30 | 19 | 20 |
该班老师准备将此次活动的捐款数据制成频数分布直方图,在制图时请你帮老师算出以下数据:
(1)计算最大值与最小值的差;
(2)若选定组距为2计算将这20个数据分成的组数;并计算将第一组的起点定为18.5时捐款数在26.5-28.5范围内的频数;
(3)计算第一组和最后一组这两个组内包含的所有样本的平均数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进一批LED灯泡与普通白炽灯炮,其进价与标价如下表,该商场购进LED灯泡与普通白炽灯炮共300个,LED灯泡按标价进行销售,而普通白炽灯炮按标价打九折销售,销售完这批灯泡后可以获利3200元。
(1)求该商场购进LED灯泡与普通白炽灯泡的数量分别为多少个?
(2)由于春节期间热销,很快将两种灯泡销售完,若该商场计划再次购进两种灯泡120个,并在不打折的情况下销售完,若销售完这批灯泡的获利不超过总进货价的28%,则最多购进LED灯泡多少个?
LED灯泡 | 普通白炽灯泡 | |
进价(元) | 45 | 25 |
标价(元) | 60 | 30 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com