
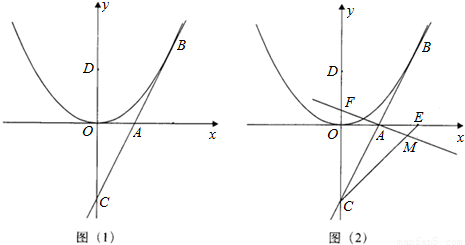
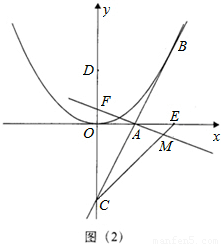
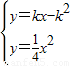 ,得点B的坐标为(2k,k2),连接OB、DE,则OB、DE均为过点D、0、E三点的圆的直径,所以,Rt△ODE≌Rt△EBO(HL),得到BE=DO=4,即可得出k值;
,得点B的坐标为(2k,k2),连接OB、DE,则OB、DE均为过点D、0、E三点的圆的直径,所以,Rt△ODE≌Rt△EBO(HL),得到BE=DO=4,即可得出k值;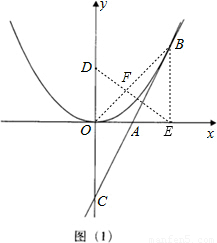 解:(1)∵直线y=kx-k2与抛物线y=ax2有唯一公共点B,
解:(1)∵直线y=kx-k2与抛物线y=ax2有唯一公共点B, ,
, x2;
x2;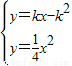 的解为
的解为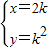 ,
,
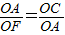 ,
,

 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:初中数学 来源: 题型:
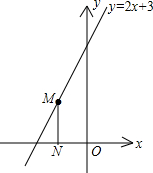 如图,点M是直线y=2x+3上的动点,过点M作MN垂直于x轴于点N,y轴上是否存在点P,使△MNP为等腰直角三角形.小明发现:当动点M运动到(-1,1)时,y轴上存在点P(0,1),此时有MN=MP,能使△NMP为等腰直角三角形.那么,在y轴和直线上是否还存在符合条件的点P和点M呢?请你写出其它符合条件的点P的坐标
如图,点M是直线y=2x+3上的动点,过点M作MN垂直于x轴于点N,y轴上是否存在点P,使△MNP为等腰直角三角形.小明发现:当动点M运动到(-1,1)时,y轴上存在点P(0,1),此时有MN=MP,能使△NMP为等腰直角三角形.那么,在y轴和直线上是否还存在符合条件的点P和点M呢?请你写出其它符合条件的点P的坐标查看答案和解析>>
科目:初中数学 来源: 题型:
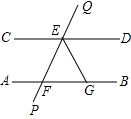 如图,AB∥CD,直线PQ分别交AB、CD于点F、E,EG是∠DEF的平分线,交AB于点G.若∠PFA=40°,那么∠EGB等于( )
如图,AB∥CD,直线PQ分别交AB、CD于点F、E,EG是∠DEF的平分线,交AB于点G.若∠PFA=40°,那么∠EGB等于( )| A、80° | B、100° | C、110° | D、120° |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,点O在直线AB上,OD是∠AOC的平分线,OE是∠COB的平分线.
如图,点O在直线AB上,OD是∠AOC的平分线,OE是∠COB的平分线.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com