
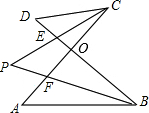
 如图,AC、BD相交于点O,BP、CP分别平分∠ABD、∠ACD,且相交于点P.
如图,AC、BD相交于点O,BP、CP分别平分∠ABD、∠ACD,且相交于点P.分析 (1)运用三角形的外角等于两个不相邻的内角的和,可得∠A+∠ABF=∠P+∠PCF,∠D+∠DCP=∠P+∠DBP,再根据角平分线的定义和等式的性质可得∠A+∠D=2∠P,从而得出关系;
(2)代入(1)的关系式可求得x的值.
解答 解:(1)∵∠CFB=∠A+∠ABF,∠CFB=∠P+∠PCF(三角形的外角等于两个不相邻的内角的和),
∴∠A+∠ABF=∠P+∠PCF(等量代换),
同理:∠D+∠DCP=∠P+∠DBP,
∴∠A+∠ABF+∠D+∠DCP=2∠P+∠PCF+∠DBP(等式性质),
∵CP,BP分别平分∠DCA,∠DBA,
∴∠ABF=∠DBP,∠DCP=∠PCF(角平分线的定义),
∴∠A+∠D=2∠P;
∠P=$\frac{1}{2}$(∠A+∠D);
(2)由∠A:∠D:∠P=2:4:x,可设∠A=2k,∠D=4k,∠P=xk(k≠0),代入∠D+∠A=2∠P可得:6k=2xk,解得x=3
点评 本题主要考查三角形外角的性质,解题的关键是在复杂图形中观察出外角和内角之间的关系,有一定的难度.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,菱形OABC的顶点O是坐标原点,顶点A在x轴的正半轴上,顶点B、C均在第一象限,OA=2,∠AOC=60°,点D在边AB上,将四边形ODBC沿直线OD翻折,使点B和点C分别落在这个坐标平面内的点B′和点C′处,且∠C′DB′=60°,则点B′的坐标是(3,-$\sqrt{3}$).
如图,菱形OABC的顶点O是坐标原点,顶点A在x轴的正半轴上,顶点B、C均在第一象限,OA=2,∠AOC=60°,点D在边AB上,将四边形ODBC沿直线OD翻折,使点B和点C分别落在这个坐标平面内的点B′和点C′处,且∠C′DB′=60°,则点B′的坐标是(3,-$\sqrt{3}$).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com