
分析 根据根与系数的关系得出a+b=m,ab=2m-2,根据勾股定理得出a2+b2=52,求出m2-2(2m-2)=25,求出m,得出方程,求出方程的解,即可得出答案.
解答 解:∵a,b是关于x的一元二次方程x2-mx+2m-2=0的两个根,
∴a+b=m,ab=2m-2,
由勾股定理得:a2+b2=52,
(a+b)2-2ab=25,
m2-2(2m-2)=25,
解得:m=7或-3,
当m=-3时,ab=2×(-3)-2=-8<0,两边长的积不能为负数,不符合题意舍去;
当m=7时,方程为x2-7x+12=0,
解得:x=4或3,
即a=4,b=3或a=3,b=4,
Rt△ABC中较小锐角的正弦值为$\frac{3}{5}$.
点评 本题考查了锐角三角函数的定义,勾股定理,根与系数的关系等知识点,能求出m的值是解此题的关键.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:解答题
 已知A、B两地相距80km,甲、乙两人沿同一条道路从A地到B地,l1,l2分别表示甲、乙两人离开A地的距离s(km)与时间t(h)之间的关系.
已知A、B两地相距80km,甲、乙两人沿同一条道路从A地到B地,l1,l2分别表示甲、乙两人离开A地的距离s(km)与时间t(h)之间的关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一种长方形餐桌的四周可以坐6人用餐(带阴影的小长方形表示1个人的位置),现把n张这样的餐桌按如图方式拼接起来.
一种长方形餐桌的四周可以坐6人用餐(带阴影的小长方形表示1个人的位置),现把n张这样的餐桌按如图方式拼接起来.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
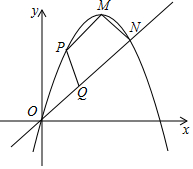 如图,二次函数y=-2x2+4x的顶点为M,一次函数y=x与抛物线分别交于O,N两点,抛物线上有一动点P,直线ON上一动点Q
如图,二次函数y=-2x2+4x的顶点为M,一次函数y=x与抛物线分别交于O,N两点,抛物线上有一动点P,直线ON上一动点Q查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com