
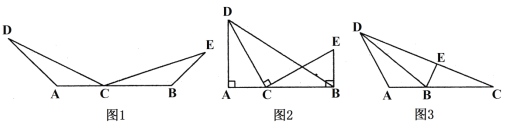
【题目】⑴如图1,点C在线段AB上,点D、E在直线AB同侧,∠A=∠DCE=∠CBE,DC=CE.求证:AC=BE.
⑵如图2,点C在线段AB上,点D、E在直线AB同侧,∠A=∠DCE=∠CBE=90°.
①求证:![]() ;②连接BD,若∠ADC=∠ABD,AC=3,BC=
;②连接BD,若∠ADC=∠ABD,AC=3,BC=![]() ,求tan∠CDB的值;
,求tan∠CDB的值;
⑶如图3,在△ABD中,点C在AB边上,且∠ADC=∠ABD,点E在BD边上,连接CE,∠BCE+∠BAD=180°,AC=3,BC=![]() ,CE=
,CE=![]() ,直接写出
,直接写出![]() 的值.
的值.
【答案】(1)见解析;(2)①见解析;②![]() ;(3)
;(3)![]() .
.
【解析】
(1)利用AAS证明![]() 可得AC=BE;
可得AC=BE;
(2)①先证明△DAC∽△CBE,再利用相似三角形的性质可得![]() ;
;
②根据∠A=∠DCE=∠CBE=90°,∠ADC=∠ABD,可推出△ADC∽△ADB,从而求出相应的线段长度,得到tan∠CDB的值.
(3)根据∠ADC=∠ABD,可推出△ADC∽△ADB,从而得到AD的长,根据∠BCE+∠BAD=180°,以E为圆心,EC长为半径画弧,交BC于点H,连接EH,可得EH=EC,∠EHC=∠ECB=∠ADC+∠DCA,可得△BEH∽△ADC,则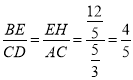 .
.
(1)证明:如图1,
![]() ,
,![]()
又![]() ,
,![]()
![]()
又![]()
![]()
![]()
(2)①证明:∵∠DCA+∠DCE+∠ECB=180°,
∠DCA+∠A+∠CDA=180°,∠A=∠DCE,
∴∠ADC=∠ECB,
∵∠A=∠B,
∴△DAC∽△CBE,
![]()
②如图2,
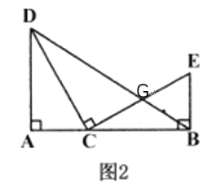
∵∠ADC=∠DBA,∠A=∠A,
∴△ADC∽△ABD,
![]()
AB=AC+BC=![]()
∴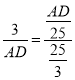
解得AD=5,
![]()
设∠DBA=∠CDA=α,
∴∠CDG=90-2α,
∴∠CGD=2α,
∴∠GCB=∠GBC=α,
∴CG=GB,
设CG=GB=x,
![]()
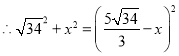
解得![]()
![]()
(3)如图3,
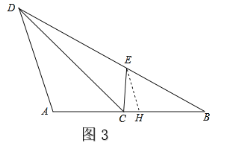
∵∠ADC=∠B,∠A=∠A,
∴△ADC∽△ADB,
![]()
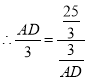
解得AD=5,
∵∠BCE+∠BAD=180°,∠ADC+∠DCA+∠BAD=180°,
∴∠ADC+∠DCA=∠BCE,
以E为圆心,EC长为半径画弧,交BC于点H,连接EH,
∴EH=EC,∠EHC=∠ECB=∠ADC+∠DCA,
∵∠B=∠ADC,
∴∠BEH=∠ACD,
∴△BEH∽△ADC,
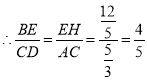
故答案为:![]()


科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于A、B两点(A在B的左侧),与y轴交于点N,过A点的直线l:
与x轴交于A、B两点(A在B的左侧),与y轴交于点N,过A点的直线l:![]() 与y轴交于点C,与抛物线
与y轴交于点C,与抛物线![]() 的另一个交点为D,已知
的另一个交点为D,已知![]() ,P点为抛物线
,P点为抛物线![]() 上一动点(不与A、D重合).
上一动点(不与A、D重合).
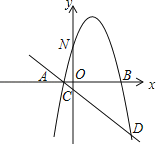
(1)求抛物线和直线l的解析式;
(2)当点P在直线l上方的抛物线上时,过P点作PE∥x轴交直线l于点E,作![]() 轴交直线l于点F,求
轴交直线l于点F,求![]() 的最大值;
的最大值;
(3)设M为直线l上的点,探究是否存在点M,使得以点N、C,M、P为顶点的四边形为平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC 为等腰直角三角形,∠ACB=90°,点 M 为 AB 边的中点,点 N 为射线 AC 上一点,连接 BN,过点 C 作 CD⊥BN 于点 D,连接 MD,作∠BNE=∠BNA,边 EN 交射线 MD 于点 E,若 AB=20![]() ,MD=14
,MD=14![]() ,则 NE 的长为___.
,则 NE 的长为___.
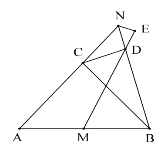
查看答案和解析>>
科目:初中数学 来源: 题型:
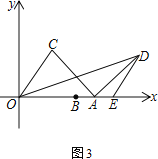
【题目】已知,点A(8,0)、B(6,0).将线段OB绕着原点O逆时针方向旋转角度α到OC,连接AC.将AC绕着点A顺时针方向旋转角度β至AD,连接OD
(1)当α=30°,β=60°时,求OD的长
(2)当α=60°,β=120°时,求OD的长
(3)已知E(10,0),当β=90°时,改变的大小,求ED的最大值
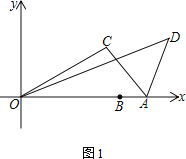
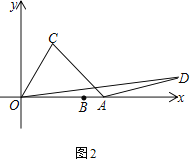
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查.调查结果显示,支付方式有:A微信、B支付宝、C现金、D其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
(1)本次一共调查了多少名购买者?
(2)请补全条形统计图;在扇形统计图中A种支付方式所对应的圆心角为 度.
(3)若该超市这一周内有1600名购买者,请你估计使用A和B两种支付方式的购买者共有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着中央电视台《朗读者》节目的播出,“朗读”为越来越多的同学所喜爱,西宁市某中学计划在全校开展“朗读”活动,为了了解同学们对这项活动的参与态度,随机对部分学生进行了一次调查,调查结果整理后,将这部分同学的态度划分为四个类别:![]() .积极参与,
.积极参与,![]() .一定参与,
.一定参与,![]() .可以参与,
.可以参与,![]() .不参与.根据调查结果制作了如下不完整的统计表和统计图.
.不参与.根据调查结果制作了如下不完整的统计表和统计图.
学生参与“朗读”的态度统计表
类别 | 人数 | 所占百分比 |
| 18 |
|
| 20 |
|
|
|
|
| 4 |
|
合计 |
|
|
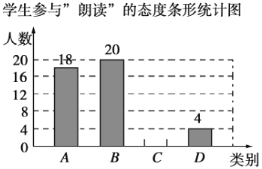
请你根据以上信息,解答下列问题:
(1)![]() ______,
______,![]() ______,并将条形统计图补充完整;
______,并将条形统计图补充完整;
(2)该校有1500名学生,如果“不参与”的人数不超过150人时,“朗读”活动可以顺利开展,通过计算分析这次活动能否顺利开展?
(3)“朗读”活动中,九年级一班比较优秀的四名同学恰好是两男两女,从中随机选取两人在班级进行朗读示范,试用画树状图法或列表法求所选两人都是女生的概率,并列出所有等可能的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在直角坐标系中,矩形![]() 的边
的边![]() 在
在![]() 轴上,点
轴上,点![]() 在原点,
在原点,![]() .若矩形以每秒2个单位长度沿
.若矩形以每秒2个单位长度沿![]() 轴正方向作匀速运动.同时点
轴正方向作匀速运动.同时点![]() 从点
从点![]() 出发以每秒1个单位长度沿
出发以每秒1个单位长度沿![]() 的路线作匀速运动,当
的路线作匀速运动,当![]() 点运动到
点运动到![]() 点时停止运动,矩形
点时停止运动,矩形![]() 也随之停止运动.设
也随之停止运动.设![]() 点运动时间为
点运动时间为![]() (秒).
(秒).
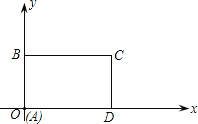
(1)当![]() 时,求出点
时,求出点![]() 的坐标;
的坐标;
(2)若![]() 的面积为
的面积为![]() ,试求出
,试求出![]() 与
与![]() 之间的函数关系式(并写出相应的自变量
之间的函数关系式(并写出相应的自变量![]() 的取值范围).
的取值范围).
(3)画出题(2)所列的函数的大致图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
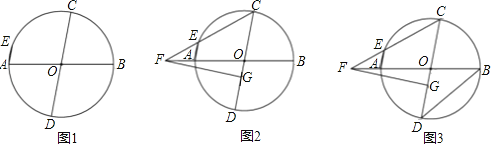
【题目】已知,在⊙O中,AB、CD是直径,弦AE∥CD.
(1)如图1,求证:![]() ;
;
(2)如图2,直线EC与直线AB交于点F,点G在OD上,若FO=FG,求证:△CFG是等腰三角形;
(3)如图3,在(2)的条件下,连接BD,若AE+CD=![]() BD,DG=4,求线段FC的长.
BD,DG=4,求线段FC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1,在矩形 ABCD 中,AB=8,AD=10,E 是 CD 边上一点,连接 AE,将矩形 ABCD 沿 AE 折叠,顶点 D 恰好落在 BC 边上点 F 处,延长 AE 交 BC 的延长线于点G.
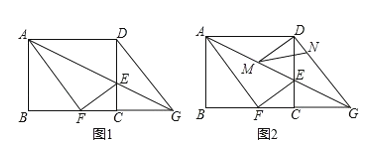
(1)求线段 CE 的长;
(2)如图 2,M,N 分别是线段 AG,DG 上的动点(与端点不重合),且∠DMN=∠DAM, 设 DN=x.
①求证四边形 AFGD 为菱形;
②是否存在这样的点 N,使△DMN 是直角三角形?若存在,请求出 x 的值;若不存在, 请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com