
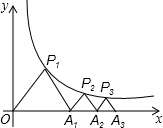
 如图,点P1(x1,y1)、P2(x2,y2)、P3(x3,y3)、…、Pn(xn,yn)、Pn+1(xn+1、yn+1)(n为正整数)在反比例函数y=$\frac{8}{x}$(x>0)的图象像上,且x1=2,xn+1=xn+2,分别连接OP1、OP2、OP3、…、OPn、OPn+1;构成若干个三角形,记△P1OP2的面积为S1,△P2OP3的面积为S2,…,依此类推,则Sn=$\frac{16n-8}{n(n-1)}$(用含有n的代数式表示)
如图,点P1(x1,y1)、P2(x2,y2)、P3(x3,y3)、…、Pn(xn,yn)、Pn+1(xn+1、yn+1)(n为正整数)在反比例函数y=$\frac{8}{x}$(x>0)的图象像上,且x1=2,xn+1=xn+2,分别连接OP1、OP2、OP3、…、OPn、OPn+1;构成若干个三角形,记△P1OP2的面积为S1,△P2OP3的面积为S2,…,依此类推,则Sn=$\frac{16n-8}{n(n-1)}$(用含有n的代数式表示) 分析 如图,连接P1P2,过点P1作P1H⊥x轴于点H,过点P2E⊥x轴于点E,由反比例函数系数k的几何意义得到:S1=S梯形P1HEP2,然后结合梯形的面积公式和反比例函数图象上点的坐标特征进行解题.
解答 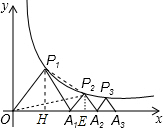 解:如图,连接P1P2,过点P1作P1H⊥x轴于点H,过点P2E⊥x轴于点E,
解:如图,连接P1P2,过点P1作P1H⊥x轴于点H,过点P2E⊥x轴于点E,
∵点P1(x1,y1)、P2(x2,y2)在反比例函数y=$\frac{8}{x}$(x>0)的图象像上,
∴S${\;}_{O{P}_{1}H}$=S${\;}_{△O{P}_{2}E}$=$\frac{1}{2}$×8=4.
∴S1=S梯形P1HEP2,
又∵当x1=2时,y1=4,即P1(2,4).
则x2=x1+2=4,y2=$\frac{8}{4}$=2,即P2(4,2).
所以S1=$\frac{4+2}{2}$×2=6;
同理,S2=$\frac{\frac{8}{2+(3-1)×2}+\frac{8}{2+(2-1)×2}}{2}$×2=$\frac{10}{3}$,
S3=$\frac{\frac{8}{2+(4-1)×2}+\frac{8}{2+(3-1)×2}}{2}$×2=$\frac{7}{3}$,
…
Sn=$\frac{\frac{8}{2+(n-1)×2}+\frac{8}{2+(n-2)×2}}{2}$×2=$\frac{16n-8}{n(n-1)}$.
故答案是:$\frac{16n-8}{n(n-1)}$.
点评 本题考查了反比例函数图象上点的坐标特征.根据图形得到S1=S梯形P1HEP2是解题的突破口.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
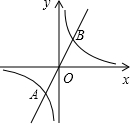 如图,已知正比例函数y=ax(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象的一个交点为A(-1,2-k2),另一个交点为B,且A,B关于原点O对称.
如图,已知正比例函数y=ax(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象的一个交点为A(-1,2-k2),另一个交点为B,且A,B关于原点O对称.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
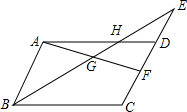 如图,在?ABCD中,DH=$\frac{1}{2}$AH,点F是边CD的中点,
如图,在?ABCD中,DH=$\frac{1}{2}$AH,点F是边CD的中点,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
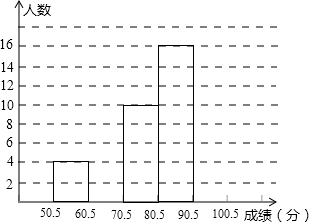 为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取整数,满分为100分)进行统计.请你根据尚未完成的频数分布表和频数分布直方图,解答下列问题:
为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取整数,满分为100分)进行统计.请你根据尚未完成的频数分布表和频数分布直方图,解答下列问题:| 分组 | 频数 | 频率 |
| 50.3-60.5 | 4 | 0.08 |
| 60.3-70.5 | 8 | 0.16 |
| 70.3-80.5 | 10 | 0.20 |
| 80.3-90.5 | 16 | 0.32 |
| 90.3-100.5 | 12 | 0.24 |
| 合计 | 50 | 1.00 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com