
| A. | $\sqrt{4\frac{9}{25}}$=$\sqrt{4}$×$\sqrt{\frac{9}{25}}$=2×$\sqrt{\frac{3}{5}}$=$\frac{6}{5}$ | B. | $\sqrt{4{1}^{2}-4{0}^{2}}$=$\sqrt{4{1}^{2}}$-$\sqrt{4{0}^{2}}$=41-40=1 | ||
| C. | 2$\sqrt{3}$×(-5$\sqrt{27}$)=-2×5×$\sqrt{3×27}$=-90 | D. | -3$\sqrt{2}$=$\sqrt{(-3)^{2}×2}$=$\sqrt{18}$ |
分析 根据二次根式的性质计算判断即可.
解答 解:A、$\sqrt{4\frac{9}{25}}=\sqrt{\frac{109}{25}}=\frac{\sqrt{109}}{5}$,错误;
B、$\sqrt{4{1}^{2}-4{0}^{2}}=\sqrt{(41-40)(41+40)}=\sqrt{81}=9$,错误;
C、$2\sqrt{3}×(-5\sqrt{27})=-10\sqrt{3×27}=-10×9=-10$,正确;
D、$-3\sqrt{2}=-\sqrt{{3}^{2}×2}=-\sqrt{18}$,错误;
故选C.
点评 此题考查二次根式的化简,关键是根据二次根式的性质计算.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:选择题
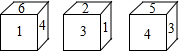 有一正方体,六个面上分别写有数字1、2、3、4、5、6,有三个人从不同的角度观察的结果如图所示.如果记1的对面的数字为a,3的对面的数字为b,那么a+b的值为( )
有一正方体,六个面上分别写有数字1、2、3、4、5、6,有三个人从不同的角度观察的结果如图所示.如果记1的对面的数字为a,3的对面的数字为b,那么a+b的值为( )| A. | 3 | B. | 7 | C. | 8 | D. | 11 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com