
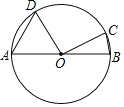
【题目】如图,AB是⊙O的直径,点D,C在⊙O上,∠DOC=90°,AD=![]() ,BC=1,则⊙O的半径为( )
,BC=1,则⊙O的半径为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:初中数学 来源: 题型:
【题目】矩形OABC的边OA、OC分别在y轴和x轴的正半轴上,且长分别为m、4m,D为AB的中点,抛物线y=﹣x2+bx+c经过点A、点D.
(1)当m=1时,求抛物线y=﹣x2+bx+c的函数关系式;
(2)延长BC至点E,连接OE,若OD平分∠AOE,抛物线与线段CE相交,求抛物线的顶点P到达最高位置时的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),某数学活动小组经探究发现:在⊙O中,直径AB与弦CD相交于点P,此时PA· PB=PC·PD
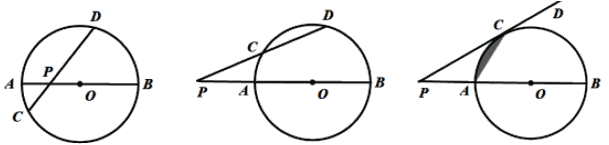
(1)如图(2),若AB与CD相交于圆外一点P, 上面的结论是否成立?请说明理由.
(2)如图(3),将PD绕点P逆时针旋转至与⊙O相切于点C, 直接写出PA、PB、PC之间的数量关系.
(3)如图(3),直接利用(2)的结论,求当 PC= ![]() ,PA=1时,阴影部分的面积.
,PA=1时,阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
已知实数m,n满足(2m2+n2+1)(2m2+n2-1)=80,试求2m2+n2的值.
解:设2m2+n2=t,则原方程变为(t+1)(t-1)=80,整理得t2-1=80,t2=81,
所以t=土9,因为2m2+n2>0,所以2m2+n2=9.
上面这种方法称为“换元法”,把其中某些部分看成一个整休,并用新字母代替(即换元),则能使复杂的问题简单化.
根据以上阅读材料内容,解决下列问题,并写出解答过程.
(1)已知实数x、y,满足(2x2+2y2+3)(2x2+2y2-3)=27,求x2+y2的值.
(2)已知Rt△ACB的三边为a、b、c(c为斜边),其中a、b满足(a2+b2)(a2+b2-4)=5,求Rt△ACB外接圆的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】襄阳市精准扶贫工作已进入攻坚阶段.贫困户张大爷在某单位的帮扶下,把一片坡地改造后种植了优质水果蓝莓,今年正式上市销售.在销售的30天中,第一天卖出20千克,为了扩大销量,采取了降价措施,以后每天比前一天多卖出4千克.第x天的售价为y元/千克,y关于x的函数解析式为![]() 且第12天的售价为32元/千克,第26天的售价为25元/千克.已知种植销售蓝莓的成木是18元/千克,每天的利润是W元(利润=销售收入﹣成本).
且第12天的售价为32元/千克,第26天的售价为25元/千克.已知种植销售蓝莓的成木是18元/千克,每天的利润是W元(利润=销售收入﹣成本).
(1)m= ,n= ;
(2)求销售蓝莓第几天时,当天的利润最大?最大利润是多少?
(3)在销售蓝莓的30天中,当天利润不低于870元的共有多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
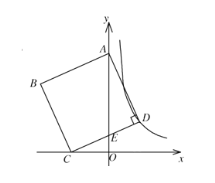
【题目】如图,在平面直角坐标系中,正方形ABCD的面积为20,顶点A在y轴上,顶点C在x轴上,顶点D在双曲线![]() 的图象上,边CD交y轴于点E,若
的图象上,边CD交y轴于点E,若![]() ,则k的值为______.
,则k的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
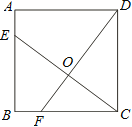
【题目】如图,已知正方形ABCD的边长为4,点E、F分别在边AB、BC上,且AE=BF=1,CE、DF交于点O.下列结论:①∠DOC=90°, ②OC=OE, ③tan∠OCD =![]() ,④
,④![]() 中,正确的有( )
中,正确的有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级一班和二班各派出10名学生参加一分钟跳绳比赛,成绩如下表:
跳绳成绩(个) | 132 | 133 | 134 | 135 | 136 | 137 |
一班人数(人) | 1 | 0 | 1 | 5 | 2 | 1 |
二班人数(人) | 0 | 1 | 4 | 1 | 2 | 2 |
(1)两个班级跳绳比赛成绩的众数、中位数、平均数、方差如下表:
众数 | 中位数 | 平均数 | 方差 | |
一班 | a | 135 | 135 | c |
二班 | 134 | b | 135 | 1.8 |
表中数据a= ,b= ,c= ;
(2)请用所学的统计知识,从两个角度比较两个班跳绳比赛的成绩.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com