
【题目】已知二次函数y=x2+bx+c的图象过点A(﹣3,0)和点B(1,0),且与y轴交于点C,D点在抛物线上且横坐标是﹣2.
(1)求抛物线的解析式;
(2)抛物线的对称轴上有一动点P,求出PA+PD的最小值.

【答案】(1)y=x2+2x﹣3;(2)![]()
【解析】试题分析: (1)把A(-3,0)和点B(1,0),代入y=x2+bx+c,建立关于b,c的二元一次方程组,求出b,c即可;
(2)先求出抛物线的对称轴,又因为A,B关于对称轴对称,所以连接BD与对称轴的交点即为所求P点.
试题解析:
(1)将A(-3,0),B(1,0)代入y=x2+bx+c,
得![]() ,解得
,解得![]()
∴y=x2+2x-3;
(2)∵y=x2+2x-3=(x+1)2-4
∴对称轴x=-1,
又∵A,B关于对称轴对称,
∴连接BD与对称轴的交点即为所求P点.
过D作DF⊥x轴于F将x=-2代入y=x2+2x-3,
则y=4-4-3=-3,
∴D(-2,-3)
∴DF=3, BF=1-(-2)=3
Rt△BDF中,BD=![]()
∵PA=PB,
∴PA+PD=BD=3![]()
故PA+PD的最小值为![]() .
.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】探究并解决问题:
探究
倍延三角形的一条中线,我们可以发现一些有用的结论.
已知,如图①所示,AD为△ABC的中线,延长AD到E,使AD=DE,连接BE、CE.
(1)求证:AB∥CE.

(2)请再写出两条不同类型的结论.
解决问题
如图所示②,分别以△ABC的边AB和AC为边,向三角形的外侧作两个等腰直角三角形,AB=AD,AC=AE,∠BAD = ∠CAE=90°,点M为BC的中点,连接DE,AM,试问线段AM、DE之间存在什么关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的周长为16,D, E,F分别为AB, BC,AC的中点,M,N,P分别为DE, EF,DF的中点,则△MNP的周长为____;如果△ABC,△DEF,△MNP分别为第1个,第2个,第3个三角形,按照上述方法继续做三角形,那么第n个三角形的周长是___.
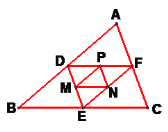
查看答案和解析>>
科目:初中数学 来源: 题型:
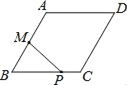
【题目】如图,菱形ABCD中,AB=2,∠B=60°,M为AB的中点.动点P在菱形的边上从点B出发,沿B→C→D的方向运动,到达点D时停止.连接MP,设点P运动的路程为x,MP 2=y,则表示y与x的函数关系的图象大致为( )
A. 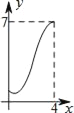 B.
B. 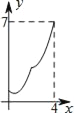 C.
C. 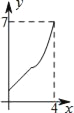 D.
D. 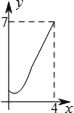
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举办了一次趣味数学竞赛,满分100分,学生得分均为整数,达到成绩60分及以上为合格,达到90分及以上为优秀,这次竞赛中,甲乙两组学生成绩如下,甲组:30,60,60,60,60,60,70,90,90,100 ;乙组:50,60,60,60,70,70,70,70,80,90.
(1)以上成绩统计分析表中a=______分,b=______分,c=_______分;
组别 | 平均数 | 中位数 | 方差 | 合格率 | 优秀率 |
甲组 | 68分 | a | 376 | 30% | |
乙组 | b | c | 90% |
(2)小亮同学说:这次竞赛我得了70分,在我们小组中属于中游略偏上,观察上面表格判断,小亮可能是甲乙哪个组的学生?并说明理由
(3)计算乙组的方差和优秀率,如果你是该校数学竞赛的教练员,现在需要你选一组同学代表学校参加复赛,你会选择哪一组?并说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种流感病毒,有一人患了这种流感,在每轮传染中一人将平均传给x人.
(1)求第一轮后患病的人数;(用含x的代数式表示)
(2)在进入第二轮传染之前,有两位患者被及时隔离并治愈,问第二轮传染后总共是否会有21人患病的情况发生,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆有50个房间供游客居住,当每个房间每天的定价为180元时,房间会全部住满;当每个房间每天的定价每增加10元时,就会有一个房间空闲.如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用.
(1)若每个房间定价增加40元,则这个宾馆这一天的利润为多少元?
(2)若宾馆某一天获利10640元,则房价定为多少元?
(3)房价定为多少时,宾馆的利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加强中小学生安全和禁毒教育,某校组织了“防溺水、交通安全、禁毒”知识竞赛,为奖励在竞赛中表现优异的班级,学校准备从体育用品商场一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),购买1个足球和1个篮球共需159元;足球单价是篮球单价的2倍少9元.
(1)求足球和篮球的单价各是多少元?
(2)根据学校实际情况,需一次性购买足球和篮球共20个,但要求购买足球和篮球的总费用不超过1550元,学校最多可以购买多少个足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
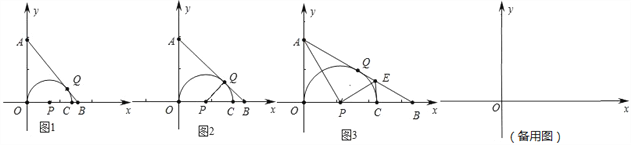
【题目】平面直角坐标系中,A(0,4),点P从原点O开始向x轴正方向运动,设P点横坐标为m,以点P为圆心,PO为半径作⊙P交x 轴另一点为C,过点A作⊙P的切线交 x轴于点B,切点为Q.
(1)如图1,当B点坐标为(3,0)时,求m;
(2)如图2,当△PQB为等腰三角形时,求m;
(3)如图3,连接AP,作PE⊥AP交AB于点E,连接CE,求证:CE是⊙P的切线;
(4)若在x轴上存在点M(8,0),在点P整个运动过程中,求MQ的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com