
【题目】每年11月的最后一个星期四是感恩节,小龙调查了初三年级部分同学在感恩节当天将以何种方式表达感谢帮助过自己的人.他将调查结果分为如下四类:A类﹣﹣当面致谢;B类﹣﹣打电话;C类﹣﹣发短信息或微信;D类﹣﹣写书信.他将调查结果绘制成如图不完整的扇形统计图和条形统计图:
请你根据图中提供的信息完成下列各题: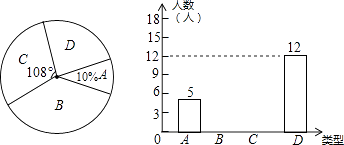
(1)补全条形统计图;
(2)在A类的同学中,有3人来自同一班级,其中有1人学过主持.现准备从他们3人中随机抽出两位同学主持感恩节主题班会课,请你用树状图或表格求出抽出的两人都没有学过主持的概率.
【答案】
(1)解:由题意可知总人数=5÷10%=50(人),所以D类所占的百分比为12÷50×100%=24%,C所占的百分比= ![]() =30%,所以C所占的人数=50×30%=15(人);
=30%,所以C所占的人数=50×30%=15(人);
B所占的百分比=1﹣10%﹣24%﹣30%=36%,B所占的人数=50×36%=18(人),由此补全统计图可得:
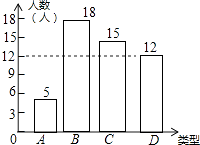
(2)解:设两个没学过主持的学生别标记为A1,A2,学过主持的学生标记为B1,列表如下:
A1 | A2 | B1 | |
A1 | (A1,A2) | (A1,B1) | |
A2 | (A2,A1) | (A2,B1) | |
B1 | (B1,A1) | (B1,A2) |
P(两人都没有学过主持)= ![]() =
= ![]()
【解析】(1)由A类的人数和百分比求出总人数,即可求出D类所占的百分比、C所占的百分比、C所占的人数、B所占的百分比、B所占的人数。就可补全统计图。
(2)先设两个没学过主持的学生别标记为A1,A2,学过主持的学生标记为B1再画出树状图或列表,根据概率公式即可求解。
【考点精析】利用扇形统计图和条形统计图对题目进行判断即可得到答案,需要熟知能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况;能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况.


科目:初中数学 来源: 题型:
【题目】如图,在正方形纸片ABCD中,EF∥AD,M,N是线段EF的六等分点,若把该正方形纸片卷成一个圆柱,使点A与点D重合,此时,底面圆的直径为10cm,则圆柱上M,N两点间的距离是cm.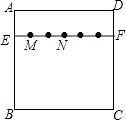
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:一组数据x1,x2,x3,x4,x5的平均数是2,方差是![]() ,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是( )
,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是( )
A. 2,![]() B. 2,1 C. 4,
B. 2,1 C. 4,![]() D. 4,3
D. 4,3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
某商场用8万元购进一批新款衬衫,上架后很快销售一空,商场又紧急购进第二批这种衬衫,数量是第一次的2倍,但进价涨了4元/件,结果共用去17.6万元.
(1)该商场第一批购进衬衫多少件?
(2)商场销售这种衬衫时,每件定价都是58元,剩至150件时按八折出售,全部售完.售完这两批衬衫,商场共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
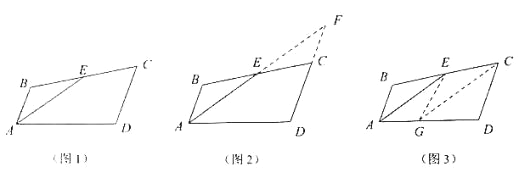
小明遇到这样一个问题:如图 1,在四边形 ABCD 中,E 是 BC 的中点,AE 是∠BAD 的平分线,AB∥DC,求证:AD=AB+DC. 小明发现以下两种方法:
方法 1:如图 2,延长 AE、DC 交于点 F;
方法 2:如图 3,在 AD 上取一点 G 使 AG=AB,连接 EG、CG.
(1)根据阅读材料,任选一种方法,证明:AD=AB+DC; 用学过的知识或参考小明的方法,解决下面的问题:
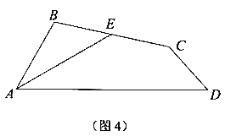
(2)如图 4,在四边形 ABCD 中,AE 是∠BAD 的平分线,E 是 BC 的中点,∠BAD=60°,∠ABC=180°-![]() ∠BCD,求证:CD=CE.
∠BCD,求证:CD=CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是连续十周测试甲、乙两名运动员体能情况的折线统计图,教练组规定:体能测试成绩70分以上(包括70分)为合适.
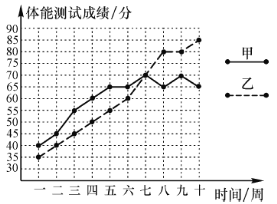
(1)请根据图中所提供的信息填写下表:
平均数 | 中位数 | 体能测试成绩合格次数(次) | |
甲 | 65 | ||
乙 | 60 |
(2)请从下面两个不同的角度对运动员体能测试结果进行判断:①依据平均数与成绩合格的次数比较甲和乙,哪个的体能测试成绩较好;②依据平均数与中位数比较甲和乙,哪个的体能测试成绩较好;
(3)依据折线统计图和成绩合格的次数,分析哪位运动员体能训练的效果较好.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解
(探究与发现)
在一次数学探究活动中,数学兴趣小组通过探究发现可以通过用“两数的差”来表示“数轴上两点间的距离”如图1中三条线段的长度可表示为:AB=4-2=2,CB=4-(-2)=6,DC=-2-(-4)=2,…结论:数轴上任意两点表示的数为分别a,b(b>a),则这两个点间的距离为b-a(即:用较大的数减去较小的数)

(理解与运用)
(1)如图2,数轴上E、F两点表示的数分别为-2,-5,试计算:EF=______,AF=______;
(2)在数轴上分别有三个点M,N,H三个点其中M表示的数为-18,点N表示的数为2018,已知点H为线段MN中点,若点H表示的数m,请你求出m的值;
(拓展与延伸)
(3)如图3,点A表示数x,点B表示-1,点C表示3x+8,且AB=![]() BC,求点A和点C分别表示什么数.
BC,求点A和点C分别表示什么数.
(4)在(3)条件下,在图3的数轴上是否存在满足条件的点D,使DA+DC=3DB,若存在,请直接写出点D表示的数;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com