
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线交AB于N,交AC于M. 
(1)若∠B=70°,则∠NMA的度数是 .
(2)连接MB,若AB=8cm,△MBC的周长是14cm.
①求BC的长;
②在直线MN上是否存在点P,使由P,B,C构成的△PBC的周长值最小?若存在,标出点P的位置并求△PBC的周长最小值;若不存在,说明理由.
【答案】
(1)50°
(2)解:猜想的结论为:∠NMA=2∠B﹣90°.
理由:∵AB=AC,
∴∠B=∠C,
∴∠A=180°﹣2∠B,
又∵MN垂直平分AB,
∴∠NMA=90°﹣∠A=90°﹣(180°﹣2∠B)=2∠B﹣90°.
如图:
①∵MN垂直平分AB.
∴MB=MA,
又∵△MBC的周长是14cm,
∴AC+BC=14cm,
∴BC=6cm.
②当点P与点M重合时,PB+CP的值最小,最小值是8cm.

【解析】解:(1)若∠B=70°,则∠NMA的度数是 50°,
所以答案是:50°;
【考点精析】掌握线段垂直平分线的性质和等腰三角形的性质是解答本题的根本,需要知道垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;等腰三角形的两个底角相等(简称:等边对等角).


 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
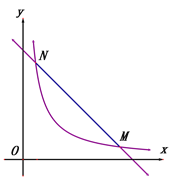
【题目】已知直线![]() (k>0)与双曲线
(k>0)与双曲线![]() (x>0)交于点M、N,且点N的横坐标为k. .
(x>0)交于点M、N,且点N的横坐标为k. .
(1) 如图1,当k=1时.
①求m的值及线段MN的长;
②在y轴上是否是否存在点Q,使∠MQN=90°,若存在,请求出点Q的坐标;若不存在,请说明理由.
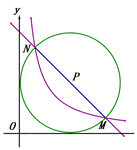
(2) 如图2,以MN为直径作⊙P,当⊙P与y轴相切时,求k值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)下列运算正确的是( )
A.5m+2m=7m2
B.﹣2m2m3=2m5
C.(﹣a2b)3=﹣a6b3
D.(b+2a)(2a﹣b)=b2﹣4a2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板中的两块直角三角尺的直角顶点O按如图方式叠放在一起.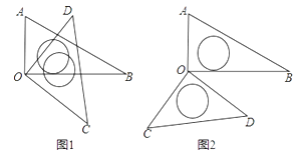
(1)如图(1)若∠BOD=35°,求∠AOC的度数,若∠AOC=135°,求∠BOD的度数。
(2)如图(2)若∠AOC=140°,求∠BOD的度数
(3)猜想∠AOC与∠BOD的大小关系,并结合图(1)说明理由.
(4)三角尺AOB不动,将三角尺COD的OD边与OA边重合,然后绕点O按顺时针或逆时针方向任意转动一个角度,当∠AOD(0°<∠AOD<90°)等于多少度时,这两块三角尺各有一条边互相垂直,直接写出∠AOD角度所有可能的值,不用说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线交AB于N,交AC于M. 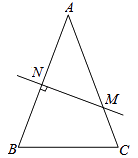
(1)若∠B=70°,则∠NMA的度数是 .
(2)连接MB,若AB=8cm,△MBC的周长是14cm.
①求BC的长;
②在直线MN上是否存在点P,使由P,B,C构成的△PBC的周长值最小?若存在,标出点P的位置并求△PBC的周长最小值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,△ABC中,D是BC边上一点,则△ABD与△ADC有一个相同的高,它们的面积之比等于相应的底之比,记为![]() (△ABD、△ADC的面积分别用记号
(△ABD、△ADC的面积分别用记号![]() 、
、![]() 表示).现有
表示).现有![]() ,则
,则![]() .
.
(2)如图2,△ABC中,E、F分别是BC、AC边上一点,且有![]() ,
, ![]() ,AE与BF相交于点G.现作EH∥BF交AC于点H.依次求
,AE与BF相交于点G.现作EH∥BF交AC于点H.依次求![]() 、
、![]() 、
、![]() 的值.
的值.
(3)如图3,△ABC中,点P在边AB上,点M、N在边AC上,且有![]() ,
, ![]() ,
,
BM、BN与CP分别相交于点R、Q.现已知△ABC的面积为1,求△BRQ的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com