
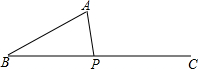
 如图,已知∠A=30°,AB=2cm,点P为∠ABC的边BC上一动点,则当BP=$\sqrt{3}$或$\frac{4}{3}$$\sqrt{3}$cm时,△BAP为直角三角形.
如图,已知∠A=30°,AB=2cm,点P为∠ABC的边BC上一动点,则当BP=$\sqrt{3}$或$\frac{4}{3}$$\sqrt{3}$cm时,△BAP为直角三角形. 分析 由于直角顶点不能确定,故应分∠APB=90°与∠BAP=90°两种情况进行分类讨论.
解答 解:当∠APB=90°时,
∵∠B=30°,AB=2cm,
∴BP1=AB•cos30°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$;
当∠BAP=90°时,
∵∠B=30°,AB=2cm,
∴BP2=$\frac{AB}{cos30°}$=$\frac{2}{\frac{\sqrt{3}}{2}}$=$\frac{4}{3}$$\sqrt{3}$.
故答案为:$\sqrt{3}$或$\frac{4}{3}$$\sqrt{3}$.
点评 本题考查的是勾股定理的逆定理,在解答此题时要注意分类讨论,不要漏解.


科目:初中数学 来源: 题型:解答题
| 时间分组 | 0.5~20.5 | 20.5~40.5 | 40.5~60.5 | 60.5~80.5 | 80.5~100.5 |
| 频数 | 20 | 25 | 30 | 15 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对某班50名同学体重情况的调查 | |
| B. | 对端午节期间市场上粽子质量情况的调查 | |
| C. | 对闽江水质情况的调查 | |
| D. | 对某类烟花爆竹燃放安全情况的调查 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 男、女生做代表的可能性一样大 | |
| B. | 男生做代表的可能性较大 | |
| C. | 女生做代表的可能性较大 | |
| D. | 男、女生做代表的可能性的大小不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com