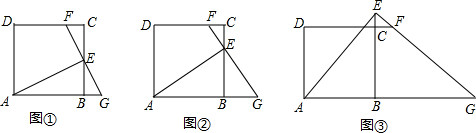
(1)解:如图所示:
.
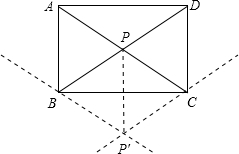
(2)PP'与BC的位置关系为:垂直.
证明:∵BP'∥PA,CP'∥PD,
∴四边形PBP'C是平行四边形,
∵点P是矩形ABCD对角线的交点,
∴BP=

BD,CP=

AC,AC=BD,AC∥BD,
∴BP=CP,
∴四边形PBP'C是菱形,
∴PP'⊥BC.
(3)证明:过点B作AP的平行线BP,过点C作PD的平行线交BP'于点P',连接PP',交BC于点M.
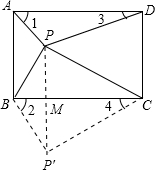
∴∠PAB+∠ABP'=180°,∠PDC+∠DCP'=180°,
以PB、BP'、P'C、CP为边构成四边形,且以BC、PP'为对角线,
∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,∠ABC=90°,
∴∠DAB+ABC=180°,∠ADC+∠DCB=180°,
∴∠1=∠2,∠3=∠4,
∴△APD≌△BP'C(ASA),
∴AP=BP'
∴四边形ABP'P是平行四边形.
∴AB∥PP',AB=PP'AP=BP',
同理可证:PD=CP',
∴∠PMC=∠ABC=90°,
∴PP'⊥BC于M,
∴以AP、BP、CP、DP为边能构成四边形,该四边形的两条对角线分别等于线段AB和BC,且互相垂直.
分析:(1)根据题意画出即可;
(2)证四边形PBP'C是平行四边形,根据矩形的性质求出BP=CP,推出四边形是菱形即可;
(3)过点B作AP的平行线BP,过点C作PD的平行线交BP'于点P',连接PP',交BC于点M,以PB、BP'、P'C、CP为边构成四边形,且以BC、PP'为对角线,证△APD≌△BP'C(ASA),推出平行四边形ABP'P,得到AB∥PP',AB=PP'AP=BP',推出PD=CP',根据等腰三角形的性质推出∠PMC=∠ABC=90°即可.
点评:本题主要考查对矩形的性质,菱形的性质和判定,平行四边形的性质和判定,全等三角形的性质和判定,等腰三角形的性质,垂线等知识点的理解和掌握,能综合运用这些性质进行推理是解此题的关键.


 .
. BD,CP=
BD,CP= AC,AC=BD,AC∥BD,
AC,AC=BD,AC∥BD,


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 19、已知五边形ABCDE如图,以点O为位似中心,将五边形ABCDE作位似变换,使原图形与它的像的位似比为2:1.
19、已知五边形ABCDE如图,以点O为位似中心,将五边形ABCDE作位似变换,使原图形与它的像的位似比为2:1.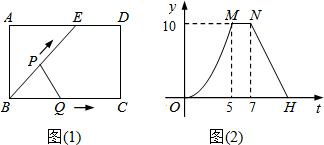 系的图象如图2(曲线OM为抛物线的一部分),则下列结论:
系的图象如图2(曲线OM为抛物线的一部分),则下列结论: