
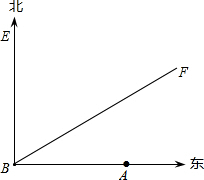
 如图,A城气象台刻得台风中心在A城正西方向160km的B处,以每小时40km的速度向北偏东60°的BF方向移动,距离台风中心100km的范围内是受台风影响的区域.
如图,A城气象台刻得台风中心在A城正西方向160km的B处,以每小时40km的速度向北偏东60°的BF方向移动,距离台风中心100km的范围内是受台风影响的区域.分析 (1)点到直线的线段中垂线段最短,故应由A点向BF作垂线,垂足为C,若AC>100则A城不受影响,否则受影响;
(2)点A到直线BF的长为100千米的点有两点,分别设为D、G,则△ADG是等腰三角形,由于AC⊥BF,则C是DG的中点,在Rt△ADC中,解出CD的长,则可求DG长,在DG长的范围内都是受台风影响,再根据速度与距离的关系则可求时间.
解答  解:(1)由A点向BF作垂线,垂足为C,
解:(1)由A点向BF作垂线,垂足为C,
在Rt△ABC中,∠ABC=30°,AB=160km,则AC=80km,
因为80<100,所以A城要受台风影响;
(2)设BF上点D,DA=100千米,则还有一点G,有AG=100千米.
因为DA=AG,所以△ADG是等腰三角形,
因为AC⊥BF,所以AC是DG的垂直平分线,CD=GC,
在Rt△ADC中,DA=100千米,AC=80千米,
由勾股定理得,CD=$\sqrt{A{D}^{2}-A{C}^{2}}$=$\sqrt{10{0}^{2}-8{0}^{2}}$=60千米,
则DG=2DC=120千米,
遭受台风影响的时间是:t=120÷40=3(小时).
点评 此题主要考查了勾股定理的应用,以及等腰三角形的性质,关键是正确构造直角三角形,利用勾股定理解决问题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2$\frac{1}{3}$ | B. | -2$\frac{1}{3}$ | C. | 0 | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 请阅读下面材料:
请阅读下面材料:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com