
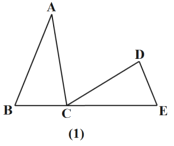
【题目】如图(1),点B、C、E在同一直线上![]() .
.
(1)求证:![]() ;
;
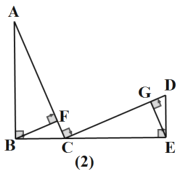
(2)若![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,请直接写出图(2)中所有与
,请直接写出图(2)中所有与![]() 互余的角.
互余的角.
【答案】(1)见解析;(2)∠ABF、∠ACB、∠D、∠GEC
【解析】
(1)利用三角形外角的性质即可得出结论;
(2)利用BF⊥AC可得∠A与∠ABF互余,根据∠ABC=90°可得∠A与∠ACB互余,再结合∠A=∠DCE可得∠A与∠D互余,最后结合GE⊥CD可得∠A与∠GEC互余.
解:(1)∵![]() ,
,
∠ACE=∠B+∠BAC,
∴∠BAC=∠DCE;
(2)∵BF⊥AC,
∴∠A+∠ABF=90°,
∵∠ABC=90°,
∴∠ACB+∠A=90°,
∵∠A=∠DCE,∠DEC=90°,
∴∠DCE+∠D=90°,
即∠A+∠D=90°,
∵GE⊥CD,
∴∠GCE+∠GEC=90°,
∴∠GEC+∠A=90°,
故与∠A互余的角有:∠ABF、∠ACB、∠D、∠GEC.


科目:初中数学 来源: 题型:
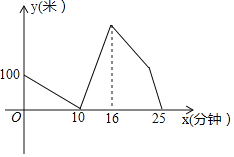
【题目】丫头和爸爸从家出发到大剧院观看“巴交有声”巴蜀中学新年演奏会,爸爸先出发,2分钟后丫头沿同一路线出发去追爸爸,当丫头追上爸爸时发现背包落在途中了,爸爸立即返回找背包,丫头继续前往大剧院,当丫头到达大剧院时,爸爸刚好找到背包并立即前往大剧院![]() 爸爸找背包的时间不计
爸爸找背包的时间不计![]() ,丫头在大剧院等了一会,没有等到爸爸,就沿同一路线返回接爸爸,最终与爸爸会合,丫头和爸爸的速度始终不变,如图是丫头和爸爸两人之间的距离
,丫头在大剧院等了一会,没有等到爸爸,就沿同一路线返回接爸爸,最终与爸爸会合,丫头和爸爸的速度始终不变,如图是丫头和爸爸两人之间的距离![]() 米
米![]() 与丫头出发的时间
与丫头出发的时间![]() 分钟
分钟![]() 的函数图象,则丫头在大剧院等了爸爸______分钟.
的函数图象,则丫头在大剧院等了爸爸______分钟.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.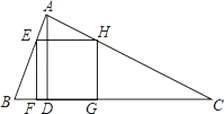
(1)求证:△AEH∽△ABC;
(2)求这个正方形的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
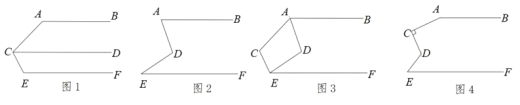
【题目】在一次数学课上,李老师让同学们独立完成课本第23页第七题选择题(2)如图 1,如果 AB∥CD∥EF,那么∠BAC+∠ACE+∠CEF=( )
A.180° B.270° C.360° D.540°
(1)请写出这道题的正确选项;
(2)在同学们都正确解答这道题后,李老师对这道题进行了改编:如图2,AB∥EF,请直接写出∠BAD,∠ADE,∠DEF之间的数量关系.
(3)善于思考的龙洋同学想:将图1平移至与图2重合(如图3所示),当AD,ED分别平分∠BAC,∠CEF时,∠ACE与∠ADE之间有怎样的数量关系?请你直接写出结果,不需要证明.
(4)彭敏同学又提出来了,如果像图4这样,AB∥EF,当∠ACD=90°时,∠BAC、∠CDE和∠DEF之间又有怎样的数量关系?请你直接写出结果,不需要证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点P(1,0).点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位至点P3,第4次向右跳动3个单位至点P4,第5次又向上跳动1个单位至点P5,第6次向左跳动4个单位至点P6,…….照此规律,点P第100次跳动至点P100的坐标是( )

A. (-26,50) B. (-25,50) C. (26,50) D. (25,50)
查看答案和解析>>
科目:初中数学 来源: 题型:
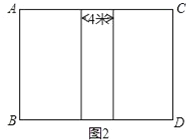
【题目】某校为学生开展拓展性课程,拟在一块长比宽多6米的长方形场地内建造由两个大棚组成的植物养殖区(如图1),要求两个大棚之间有间隔4米的路,设计方案如图2,已知每个大棚的周长为44米.
(1)求每个大棚的长和宽各是多少?
(2)现有两种大棚造价的方案,方案一是每平方米60元,超过100平方米优惠500元,方案二是每平方米70元,超过100平方米优惠总价的20%,试问选择哪种方案更优惠?

查看答案和解析>>
科目:初中数学 来源: 题型:
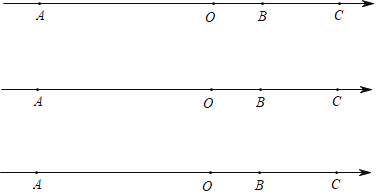
【题目】如图,已知A、B、C是数轴上的三点,点C表示的数是6,点B与点C之间的距离是4,点B与点A的距离是12,点P为数轴上一动点.
(1)数轴上点A表示的数为 .点B表示的数为 ;
(2)数轴上是否存在一点P,使点P到点A、点B的距离和为16,若存在,请求出此时点P所表示的数;若不存在,请说明理由;
(3)点P以每秒1个单位长度的速度从C点向左运动,点Q以每秒2个单位长度从点B出发向左运动,点R从点A以每秒5个单位长度的速度向右运动,它们同时出发,运动的时间为t秒,请求点P与点Q,点R的距离相等时t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.如图 1,AB∥CD,直线 EF 交 AB 于点 E,交 CD 于点 F,点 G 在 CD 上,点 P在直线 EF 左侧,且在直线 AB 和 CD 之间,连接 PE,PG.
(1) 求证: ∠EPG=∠AEP+∠PGC;
(2) 连接 EG,若 EG 平分∠PEF,∠AEP+ ∠ PGE=110°,∠PGC=![]() ∠EFC,求∠AEP 的度数.
∠EFC,求∠AEP 的度数.
(3) 如图 2,若 EF 平分∠PEB,∠PGC 的平分线所在的直线与 EF 相交于点 H,则∠EPG 与∠EHG之间的数量关系为 .
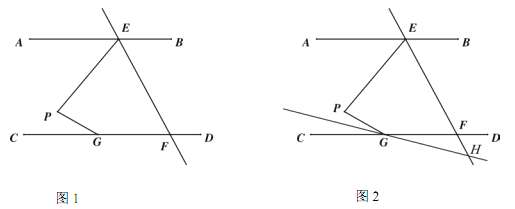
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com