
【题目】如图,在△ABC中,∠ABC=45°,AD,BE分别为BC、AC边上的高,AD、BE相交于点F,连接CF,则下列结论:①BF=AC; ②∠FCD=45°; ③若BF=2EC,则△FDC周长等于AB的长;其中正确的有( )
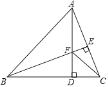
A. 0个 B. 1个 C. 2个 D. 3个
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx﹣3a经过点A(﹣1,0)、C(0,3),与x轴交于另一点B,抛物线的顶点为D.
(1)求此二次函数解析式;
(2)连接DC、BC、DB,求证:△BCD是直角三角形;
(3)在对称轴右侧的抛物线上是否存在点P,使得△PDC为等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,SABCD=24,AE平分∠BAC,交BC于E,沿AE将△ABE折叠,点B的对应点为F,连接EF并延长交AD于G,EG将ABCD分为面积相等的两部分.则S△ABE= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明购买了一部新手机,到某通讯公司咨询移动电话资费情况,准备办理入网手续,该通讯公司工作人员向他介绍两种不同的资费方案:
方案代号 | 月租费(元) | 免费时间(分) | 超过免费时间的通话费(元/分) |
一 | 10 | 0 | 0.20 |
二 | 30 | 80 | 0.15 |
(1)分别写出方案一、二中,月话费(月租费与通话费的总和)y(单位:元)与通话时间x(单位:分)的函数关系式;
(2)画出(1)中两个函数的图象;
(3)若小明月通话时间为200分钟左右,他应该选择哪种资费方案最省钱.
查看答案和解析>>
科目:初中数学 来源: 题型:
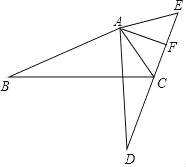
【题目】如图,∠BAD=∠CAE,AB=AD,AC=AE.且E,F,C,D在同一直线上.
(1)求证:△ABC≌△ADE;
(2)若∠B=30°,∠BAC=100°,点F是CE的中点,连结AF,求∠FAE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①如果两个三角形全等,那么这两个三角形一定成轴对称;②数轴上的点和实数一一对应;③![]() 是3的一个平方根;④两个无理数的和一定为无理数;⑤6.9
是3的一个平方根;④两个无理数的和一定为无理数;⑤6.9![]() 103精确到十分位;⑥
103精确到十分位;⑥![]() 的平方根是
的平方根是![]() 4.其中正确的__________ .(填序号)
4.其中正确的__________ .(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′的度数是( ) 
A.70°
B.35°
C.40°
D.50°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,五边形ABCDE中有一正三角形ACD,若AB=DE,BC=AE,∠E=115°,则∠BAE的度数为何?( )

A. 115 B. 120 C. 125 D. 130
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
(材料)如图,对任意符合条件的直角三角形BAC,绕其锐角顶点逆时针旋转90°得△DAE,所以∠BAE=90°,且四边形ACFD是一个正方形,它的面积和四边形ABFE面积相等,而四边形ABFE面积等于Rt△BAE和Rt△BFE的面积之和,根据图形我们就能证明勾股定理: ![]() .
.

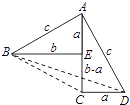
(请回答)如图是任意符合条件的两个全等的Rt△BEA和Rt△ACD拼成的,你能根据图示再写一种证明勾股定理的方法吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com