
【题目】如图所示,△DEF中,∠DEF=90°,∠D=30°,DF=16,B是斜边DF上一动点,过B作AB⊥DF于B,交边DE(或边EF)于点A,设BD=x,△ABD的面积为y,则y与x之间的函数图象大致为( )


A. (A) B. (B) C. (C) D. (D)
【答案】B
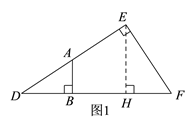
【解析】如图1和图2,过点E作EH⊥DF于点H,
∵在△DEF中,∠DEF=90°,∠D=30°,DF=16,
∴EF=8,DE=![]() ,EH=
,EH=![]() ,DH=12,HF=4,
,DH=12,HF=4,
(1)如图1,当点A在DE上时,此时点B在DH上,即![]() ,
,
∵AB⊥DF于点B,∠D=30°,BD= ![]() ,
,
∴AB=BD·tan∠D= ![]() ,
,
∴此时y=S△ABD= =![]() ,即
,即![]() ,
,
∴当![]() 时,y有最大值,此时点A与E重合;
时,y有最大值,此时点A与E重合;
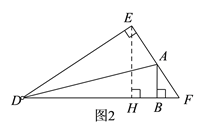
(2)如图2,当点A在EF上时,此时点B在HF上,即![]() ,
,
∵AB⊥DF于点B,∠D=30°,BD= ![]() ,
,
∴BF= ![]() ,∠ABF=90°,∠F=60°,
,∠ABF=90°,∠F=60°,
∴AB=BF·tan∠F=![]() ,
,
∴此时y=S△ABD=![]() BD·AB=
BD·AB=![]() ,即y=
,即y= ![]() ;
;
综上所述,结合二次函数的图象特征可知y随x变化而变化的图象应该是B选项中的图象.
故选B.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】积极响应市委市政府“加快建设绿水青山的美丽乐山”的号召,我市某街道决定从备选的五种树中选购一种进行栽种.为了更好地了解社情民意,工作人员在街道辖区范围内随机抽取了部分居民,进行“我最喜欢的一种树”的调查活动(每人限选其中一种树),并将调查结果整理后,绘制成如图所示两个不完整的统计图:

请根据所给信息解答以下问题:
(1)这次参与调查的居民人数为______;
(2)请将条形和扇形统计图补充完整;
(3)请计算扇形统计图中“枫树”所在扇形的圆心角度数;
(4)已知该街道辖区内现有居民2万人,请你估计这2万人中最喜欢玉兰树的有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自古以来,人类对于蜜蜂的勤劳以及蜂巢的巧妙精准无不赞扬有加.从生物学鼻祖亚里士多德,到数学家帕普斯,以及近代的生物学家达尔文都曾留下了赞美的诗句.工蜂分泌蜂蜡筑成蜂窝,作为蜂王产卵、工蜂育幼以及存放蜂蜜、花粉的贮藏室.从正面来看,蜂巢是由许多正六边形连结而成,正六边形是能够不重叠地铺满一个平面的三种正多边形之一,另外两种分别是正方形和正三角形.
(1)一根长12![]() 的铁丝分别围成正三角形,正方形,正六边形,请同学们直接写出围成图形的面积:
的铁丝分别围成正三角形,正方形,正六边形,请同学们直接写出围成图形的面积:![]() ,
,![]() ,
,![]() ;
;
(2)在(1)的条件下,比较围成图形面积的大小;
(3)通过以上计算,当面积一定时,耗材最少的图形是 (填:正三角形、正方形、正六边形).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】义安中学工会“三八妇女节”共筹集会费1800元,工会决定拿出不少于270元,但不超过300元的资金为“优秀女职工”购买纪念品,其余的钱用于给50位女职工每人买一瓶洗发液或护发素,已知每瓶洗发液比每瓶护发素贵9元,用200元恰好可以买到2瓶洗发液和5瓶护发素.
(1)求每瓶洗发液和每瓶护发素价格各是多少元?
(2)有几种购买洗发液和护发素的方案?哪种方案用于为“优秀女职工”购买纪念品的资金更充足?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线![]() 与
与![]() 轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线
轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线![]() ,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )
,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使△AMN周长最小时,则∠AMN+∠ANM的度数是________

查看答案和解析>>
科目:初中数学 来源: 题型:
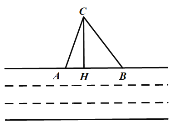
【题目】笔直的河流一侧有一旅游地C,河边有两个漂流点A.B.其中AB=AC,由于某种原因,由C到A的路现在已经不通,为方便游客决定在河边新建一个漂流点H(A,H,B在一条直线上),并新修一条路CH测得BC=5千米,CH=4干米,BH=3千米,
(1)问CH是否为从旅游地C到河的最近的路线?请通过计算加以说明;
(2)求原来路线AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八(1)班组织了一次食品安全知识竞赛,甲、乙两队各5人的成绩如表所示(10分制).
数据 | 中位数 | 众数 | 方差 | |||||
甲 | 8 | 10 | 9 | 6 | 9 | 9 | 1.84 | |
乙 | 10 | 8 | 9 | 7 | 8 | 8 | 1.04 | |
(1)补全表格中的众数和中位数
(2)并判断哪队的成绩更稳定?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知Rt△ABC中,∠ACB=90°,CA=CB=4,另有一块等腰直角三角板的直角顶点放在C处,CP=CQ=2,将三角板CPQ绕点C旋转(保持点P在△ABC内部),连接AP、BP、BQ.
(1)如图1求证:AP=BQ;
(2)如图2当三角板CPQ绕点C旋转到点A、P、Q在同一直线时,求AP的长;
(3)设射线AP与射线BQ相交于点E,连接EC,写出旋转过程中EP、EQ、EC之间的数量关系.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com