
在直角坐标平面内,二次函数图象的顶点为A(1,﹣4),且过点B(3,0).
(1)求该二次函数的解析式;
(2)将该二次函数图象向右平移几个单位,可使平移后所得图象经过坐标原点?并直接写出平移后所得图象与x轴的另一个交点的坐标.
(1)y=x2﹣2x﹣3;(2)1,(4,0).
解析试题分析:(1)有顶点就用顶点式来求二次函数的解析式;
(2)由于是向右平移,可让二次函数的y的值为0,得到相应的两个x值,算出负值相对于原点的距离,而后让较大的值也加上距离即可.
试题解析:(1)∵二次函数图象的顶点为A(1,﹣4),
∴设二次函数解析式为y=a(x﹣1)2﹣4,
把点B(3,0)代入二次函数解析式,得:
0=4a﹣4,解得a=1,
∴二次函数解析式为y=(x﹣1)2﹣4,即y=x2﹣2x﹣3;
(2)令y=0,得x2﹣2x﹣3=0,解方程,得x1=3,x2=﹣1.
∴二次函数图象与x轴的两个交点坐标分别为(3,0)和(﹣1,0),
∴二次函数图象上的点(﹣1,0)向右平移1个单位后经过坐标原点.
故平移后所得图象与x轴的另一个交点坐标为(4,0).
考点:1. 待定系数法求二次函数解析式;2.二次函数图象与几何变换.


科目:初中数学 来源: 题型:解答题
如图1,在菱形ABCD中,对角线AC、BD相交于点O,AC=8,BD=6.现有两动点P、Q分别从A、C两点同时出发,点P以每秒1个单位长的速度由点A向点D做匀速运动,点Q沿折线CB—BA向点A做匀速运动.
(1)点P将要运行路径AD的长度为 ;点Q将要运行的路径折线CB—BA的长度为 .
(2)当点Q在BA边上运动时,若点Q的速度为每秒2个单位长,设运动时间为t秒.
①求△APQ的面积S关于t的函数关系式,并求自变量t的取范围;
②求当t为何值时,S有最大值,最大值是多少?
(3)如图2,若点Q的速度为每秒a个单位长(a≤ ),当t =4秒时:
),当t =4秒时:
①此时点Q是在边CB上,还是在边BA上呢?
②△APQ是等腰三角形,请求出a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,O为坐标原点,点A、B的坐标分别为(8,0)、(0,6).动点Q从点O、动点P从点A同时出发,分别沿着OA方向、AB方向均以1个单位长度/秒的速度匀速运动,运动时间为t(秒)(0<t≤5).以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连接CD、QC.
(1)求当t为何值时,点Q与点D重合?
(2)设△QCD的面积为S,试求S与t之间的函数关系式,并求S的最大值;
(3)若⊙P与线段QC只有一个交点,请直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,﹣3)点,点P是直线BC下方的抛物线上一动点.
(1)求这个二次函数的表达式.
(2)连接PO、PC,并把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知在平面直角坐标系xoy中,二次函数y=-2x²+bx+c的图像经过点A(-3,0)和点B(0,6)。(1)求此二次函数的解析式;(2)将这个二次函数的图像向右平移5个单位后的顶点设为C,直线BC与x轴相交于点D,求∠sin∠ABD;(3)在第(2)小题的条件下,连接OC,试探究直线AB与OC的位置关系,并且说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某宾馆有30个房间供游客住宿,当每个房间的房价为每天160元时,房间会全部住满。当每个房间每天的房价每增加10元时,就会有一个房间空闲。宾馆需对游客居住的每个房间每天支出20元的各种费用。根据规定,每个房间每天的房价不得高于260元。
设每个房间的房价每天增加x元(x为10的整数倍)。
(1)设一天订住的房间数为y,直接写出y与x的函数关系式及自变量x的取值范围;
(2)设宾馆一天的利润为w元,求w与x的函数关系式;
(3)一天订住多少个房间时,宾馆的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某超市经销一种销售成本为每件20元的商品.据市场调查分析,如果按每件30元销售,一周能售出500件,若销售单价每涨1元,每周的销售量就减少10件.设销售单价为每件x元(x≥30),一周的销售量为y件.
(1)写出y与x的函数关系式及自变量x的取值范围;
(2)该超市想通过销售这种商品一周获得利润8000元,销售单价应定为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,已知点 坐标为(2,4),直线x=2与
坐标为(2,4),直线x=2与 轴相交于点
轴相交于点 ,连结
,连结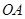 ,抛物线y=x
,抛物线y=x
 从点
从点 沿
沿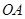 方向平移,与直线x=2交于点
方向平移,与直线x=2交于点 ,顶点
,顶点 到
到 点时停止移动.
点时停止移动.
(1)求线段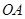 所在直线的函数解析式;
所在直线的函数解析式;
(2)设抛物线顶点 的横坐标为
的横坐标为 ,
,
①用 的代数式表示点
的代数式表示点 的坐标;
的坐标;
②当 为何值时,线段
为何值时,线段 最短;
最短;
(3)当线段 最短时,相应的抛物线上是否存在点
最短时,相应的抛物线上是否存在点 ,使△
,使△ 的面积与△
的面积与△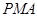 的面积相等,若存在,请求出点
的面积相等,若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com