
 已知线段m,∠a(如图).
已知线段m,∠a(如图).分析 (1)先作∠BAC=90°,再截取AB=m,然后过点B作AC的垂线,垂足为C,则△ABC满足条件;
(2)作线段AB的垂直平分线得到DE,则根据线段垂直平分线的性质得到AE=BE,接着根据等线段代换可得到△BCE的周长=AC+BC,然后利用勾股定理计算出AC即可得到△BCE的周长.
解答 解:(1)如图,△ABC为所作;
(2)如图,DE为所作,
∵DE垂直平分AB,
∴AE=BE,
∴△BCE的周长=BE+CE+BC=AE+CE+BC=AC+BC,
∵AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
∴△BCE的周长=8+6=14.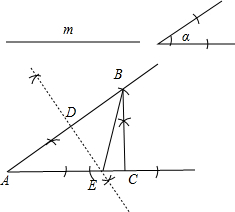
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.


 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:解答题
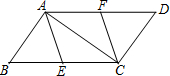 如图,E、F分别是?ABCD的边BC、AD上的中点.
如图,E、F分别是?ABCD的边BC、AD上的中点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在?ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD边上的点F.若△FDE的周长为8,△FCB的周长为22,则FC的长为7.
如图,在?ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD边上的点F.若△FDE的周长为8,△FCB的周长为22,则FC的长为7.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知一次函数y=kx+b的图象与x轴交于点A(5,0),与函数y=2x的图象交于点M,点M的横坐标为2,求点M的坐标及函数y=kx+b的表达式.
如图,已知一次函数y=kx+b的图象与x轴交于点A(5,0),与函数y=2x的图象交于点M,点M的横坐标为2,求点M的坐标及函数y=kx+b的表达式.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
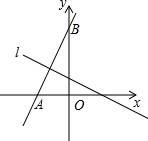 如图,己知直线y=2x+4与x轴,y轴分别交于A,B两点,则线段AB的中垂线l的函数表达式为y=$-\frac{1}{2}$x+$\frac{3}{2}$.
如图,己知直线y=2x+4与x轴,y轴分别交于A,B两点,则线段AB的中垂线l的函数表达式为y=$-\frac{1}{2}$x+$\frac{3}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
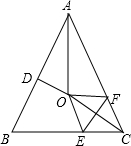 如图,在△ABC中,AB=AC,∠BAC=58°,∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠BEO的度数是64°.
如图,在△ABC中,AB=AC,∠BAC=58°,∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠BEO的度数是64°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com