
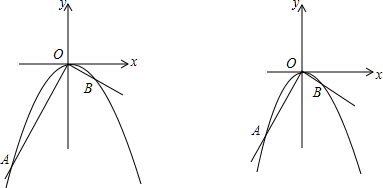
ЗжЮі ЃЈ1ЃЉШчЭМ1ЃЌзїBFЁЭxжсгкFЃЌAEЁЭxжсгкЕуEЃЌЕБx=1ЪБДњШыНтЮіЪНОЭПЩвдЧѓГіyЕФжЕЃЌДгЖјЕУГіBЕФзјБъЃЌЩшAЃЈaЃЌ-$\frac{1}{2}$a2ЃЉЃЌгЩШ§НЧаЮЯрЫЦОЭПЩвдЧѓГіAЕФКсзјБъЃЛ
ЃЈ2ЃЉЪзЯШЩшAЃЈ-mЃЌ-$\frac{1}{2}$m2ЃЉЃЈmЃО0ЃЉЃЌBЃЈnЃЌ-$\frac{1}{2}$n2ЃЉЃЈnЃО0ЃЉЃЌБэЪОГіжБЯпABНтЮіЪНжаb=-$\frac{1}{2}$mnЃЌдйРћгУЙДЙЩЖЈРэЕУГіmn=4ЃЌНјЖјЕУГіжБЯпABКуЙ§ЦфгыyжсЕФНЛЕуCЃЈ0ЃЌ-2ЃЉЃЎ
ЃЈ3ЃЉгЩЃЈ1ЃЉЕФНтЮіЪНЧѓГіЦНвЦКѓЕФНтЮіЪНЃЌЧѓГіMЁЂNЁЂGЕФзјБъзїGEЁЭxжсгкEЃЌзїЁЯMNGЕФЦНЗжЯпNPНЛGEгкPЃЌзїPFЁЭNGгкFЃЌИљОнЖдГЦжсЕФаджЪОЭПЩвдЧѓГіEЕФзјБъЃЌгЩЕШбќШ§НЧаЮЕФаджЪМАИњЙДЙЩЖЈРэОЭПЩвдЧѓГіНсТлЃЎ
НтД№ НтЃКЃЈ1ЃЉШчЭМ1ЃЌзїBFЁЭxжсгкFЃЌAEЁЭxжсгкЕуEЃЌ
ЁрЁЯAEO=ЁЯBFO=90ЁуЃЌ
ЁрЁЯEAO+ЁЯAOE=90ЁуЃЎ
ЁпЁЯAOB=90ЁуЃЌ
ЁрЁЯAOE+ЁЯBOF=90ЁуЃЌ
ЁрЁЯEAO=ЁЯBOFЃЎ
ЁпOF=1ЃЌ
ЁрBЕФКсзјБъЮЊ1ЃЌ
Ёрy=-$\frac{1}{2}$ЁС1=-$\frac{1}{2}$ЃЌ
ЁрBF=$\frac{1}{2}$ЃЌBЃЈ1ЃЌ-$\frac{1}{2}$ЃЉЃЎ
ЁпЁЯAEO=ЁЯBFOЃЌЁЯEAO=ЁЯBOFЃЌ
ЁрЁїAOEЁзЁїOBFЃЌ
Ёр$\frac{OF}{AE}=\frac{BF}{OE}$ЃЎ
ЩшAЃЈaЃЌ-$\frac{1}{2}$a2ЃЉЃЌ
ЁрEO=-aЃЌAE=$\frac{1}{2}$a2ЃЌ
Ёр$\frac{1}{\frac{1}{2}{a}^{2}}=\frac{\frac{1}{2}}{-a}$ЃЌ$\left\{\begin{array}{l}{-mk+b=-\frac{1}{2}{m}^{2}}\\{nk+b=-\frac{1}{2}{n}^{2}}\end{array}\right.$
НтЕУЃКa1=0ЃЈЩсШЅЃЉЃЌa2=-4ЃЌ
ЁрAЕФКсзјБъЮЊ-4ЃЛ
ЃЈ2ЃЉЩшAЃЈ-mЃЌ-$\frac{1}{2}$m 2ЃЉЃЈmЃО0ЃЉЃЌBЃЈnЃЌ-$\frac{1}{2}$n 2ЃЉЃЈnЃО0ЃЉЃЌ
ЩшжБЯпABЕФНтЮіЪНЮЊЃКy=kx+bЃЌ
$\left\{\begin{array}{l}{-mk+b=-\frac{1}{2}{m}^{2}Ђй}\\{nk+b=-\frac{1}{2}{n}^{2}Ђк}\end{array}\right.$ЃЌ
ЂйЁСn+ЂкЁСmЕУЃЌЃЈm+nЃЉb=-$\frac{1}{2}$ЃЈm2n+mn2ЃЉ=-$\frac{1}{2}$mnЃЈm+nЃЉЃЌ
Ёрb=-$\frac{1}{2}$mnЃЌ
ЁпOB2=n2+$\frac{1}{4}$n4ЃЌOA2=m2+$\frac{1}{4}$m4ЃЌAB2=ЃЈn+mЃЉ2+ЃЈ-$\frac{1}{2}$m2+$\frac{1}{2}$n2ЃЉ2ЃЌAB2=OA2+OB2ЃЌ
Ёрn2+$\frac{1}{4}$n4+m2+$\frac{1}{4}$m4=ЃЈn+mЃЉ2+ЃЈ-$\frac{1}{2}$m2+$\frac{1}{2}$n2ЃЉ2ЃЌ
ЛЏМђЃЌЕУmn=4
Ёрb=-$\frac{1}{2}$ЁС4=-2ЃЎ
ЁрВЛТлkЮЊКЮжЕЃЌжБЯпABКуЙ§ЕуЃЈ0ЃЌ-2ЃЉЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌДцдкЗћКЯЬѕМўЕФtЃЎ
ЁпC1ЃКy=-$\frac{1}{2}$x2ЃЌ
ЁрХзЮяЯпC1гвгввЦ1ИіЕЅЮЛКѓдкЯђЩЯвЦ2ИіЕЅЮЛЕУЕНЕФНтЮіЪНЮЊЃК
y=-$\frac{1}{2}$ЃЈx-1ЃЉ2+2ЃЌ
ЁрGЃЈ1ЃЌ2ЃЉЃЎ
ЕБy=0ЪБЃЌ-$\frac{1}{2}$ЃЈx-1ЃЉ2+2=0ЃЌ
Ёрx1=-1ЃЌx2=3ЃЎ
ЁрMN=4ЃЎ
зїGEЁЭxжсгкEЃЌ
ЁрEЃЈ1ЃЌ0ЃЉЃЌME=EN=2ЃЎEG=2ЃЌЁЯGEN=90Ёу
ЁрEG=EN=2ЃЎ
ЁргЩЙДЙЩЖЈРэЃЌЕУ
GN=2$\sqrt{2}$ЃЎ
зїЁЯMNGЕФЦНЗжЯпNPНЛGEгкPЃЌзїPFЁЭNGгкFЃЌ
ЁрЁЯPNE=ЁЯPNFЃЌЁЯPFG=ЁЯPFN=90Ёу
ЁрPE=PFЃЎЁЯGEN=ЁЯPFNЃЎ
ЁпPЃЈ1ЃЌtЃЉЃЈtЃО0ЃЉЃЌ
ЁрЕуPдкжБЯпGEЩЯЃЌдкxжсЕФЩЯЗНЃЌ
ЁрPE=PF=tЃЌGP=2-tЃЎ
дкRtЁїPENКЭRtЁїPFNжаЃЌ
$\left\{\begin{array}{l}{PN=PN}\\{PE=PF}\end{array}\right.$ЃЌ
ЁрRtЁїPENЁеRtЁїPFNЃЈHLЃЉЃЌ
ЁрEN=FNЃЎ
ЁрFN=2ЃЎ
ЁрGF=2$\sqrt{2}$-2ЃЌ
дкRtЁїGPFжаЃЌгЩЙДЙЩЖЈРэЃЌЕУ
ЃЈ2$\sqrt{2}$-2ЃЉ2+t2=ЃЈ2-tЃЉ2ЃЌ
НтЕУЃКt=2$\sqrt{2}$-2ЃЎ
ЕуЦР БОЬтПМВщСЫЖўДЮКЏЪ§ЕФаджЪЕФдЫгУЃЌЯрЫЦШ§НЧаЮЕФХаЖЈгыаджЪЕФдЫгУЃЌЦНвЦЕФаджЪЕФдЫгУЃЌЙДЙЩЖЈРэЕФдЫгУЃЌНЧЦНЗжЯпЕФаджЪЕФдЫгУЃЌШЋЕШШ§НЧаЮЕФХаЖЈгыаджЪЕФдЫгУЃЌЧаЯпЕФХаЖЈгыаджЪЕФдЫгУЃЌНтД№ЪБдЫгУЖўДЮКЏЪ§ЕФаджЪЧѓНтЪЧЙиМќЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
 ШчЭМЫљЪОЃЌе§ЗНаЮABCDЕФУцЛ§ЮЊ169cm2ЃЌСтаЮBCPQЕФУцЛ§ЮЊ156cm2ЃЎдђвѕгАВПЗжЕФУцЛ§ЪЧЃЈЁЁЁЁЃЉ
ШчЭМЫљЪОЃЌе§ЗНаЮABCDЕФУцЛ§ЮЊ169cm2ЃЌСтаЮBCPQЕФУцЛ§ЮЊ156cm2ЃЎдђвѕгАВПЗжЕФУцЛ§ЪЧЃЈЁЁЁЁЃЉ| AЃЎ | 23cm2 | BЃЎ | 33cm2 | CЃЎ | 43cm2 | DЃЎ | 53cm2 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
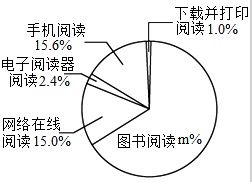 ИљОнФГбаОПдКЙЋВМЕФ2010-2014ФъЮвЙњГЩФъЙњУёдФЖСЕїВщБЈИцЕФВПЗжЯрЙиЪ§ОнЃЌЛцжЦЕФЭГМЦЭМБэШчЯТЃК
ИљОнФГбаОПдКЙЋВМЕФ2010-2014ФъЮвЙњГЩФъЙњУёдФЖСЕїВщБЈИцЕФВПЗжЯрЙиЪ§ОнЃЌЛцжЦЕФЭГМЦЭМБэШчЯТЃК| ФъЗн | ФъШЫОљдФЖСЭМЪщЪ§СПЃЈБОЃЉ |
| 2010 | 3.8 |
| 2011 | 4.1 |
| 2012 | 4.3 |
| 2013 | 4.6 |
| 2014 | 4.8 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com