
【题目】我州某养殖场计划购买甲、乙两种鱼苗600条,甲种鱼苗每条16元,乙种鱼苗每条20元,相关资料表明:甲、乙两种鱼苗的成活率为80%,90%
(1)若购买这两种鱼苗共用去11000元,则甲、乙两种鱼苗各购买多少条?
(2)若要使这批鱼苗的总成活率不低于85%,则乙种鱼苗至少购买多少条?
(3)在(2)的条件下,应如何选购鱼苗,使购买鱼苗的总费用最低?最低费用是多少?
【答案】(1)购买甲种鱼苗350条,乙种鱼苗250条;(2)300;(3)当购买甲种鱼苗300条,乙种鱼苗300条时,总费用最低,最低费用为10800元.
【解析】
试题分析:(1)设购买甲种鱼苗x条,乙种鱼苗y条,根据“购买甲、乙两种鱼苗600条,甲种鱼苗每条16元,乙种鱼苗每条20元”即可列出关于x、y的二元一次方程组,解方程组即可得出结论;
(2)设购买乙种鱼苗m条,则购买甲种鱼苗(600﹣m)条,根据“甲、乙两种鱼苗的成活率为80%,90%,要使这批鱼苗的总成活率不低于85%”即可列出关于m的一元一次不等式,解不等式即可得出m的取值范围;
(3)设购买鱼苗的总费用为w元,根据“总费用=甲种鱼苗的单价×购买数量+乙种鱼苗的单价×购买数量”即可得出w关于m的函数关系式,根据一次函数的性质结合m的取值范围,即可解决最值问题.
试题解析:(1)设购买甲种鱼苗x条,乙种鱼苗y条,根据题意得:![]() ,解得:
,解得:![]() .
.
答:购买甲种鱼苗350条,乙种鱼苗250条.
(2)设购买乙种鱼苗m条,则购买甲种鱼苗(600﹣m)条,根据题意得:90%m+80%(600﹣m)≥85%×600,解得:m≥300.
答:购买乙种鱼苗至少300条.
(3)设购买鱼苗的总费用为w元,则w=20m+16(600﹣m)=4m+9600,∵4>0,∴w随m的增大而增大,又∵m≥300,∴当m=300时,w取最小值,w最小值=4×300+9600=10800(元).
答:当购买甲种鱼苗300条,乙种鱼苗300条时,总费用最低,最低费用为10800元.


 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:
【题目】如图(1),将两块直角三角尺的直角顶点C叠放在一起,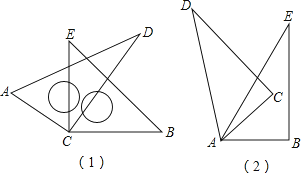
(1)若∠DCE=25°,∠ACB=?;若∠ACB=150°,则∠DCE=?;
(2)猜想∠ACB与∠DCE的大小有何特殊关系,并说明理由;
(3)如图(2),若是两个同样的直角三角尺60°锐角的顶点A重合在一起,则∠DAB与∠CAE的大小又有何关系,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为实现区域教育均衡发展,我市计划对某县A、B两类薄弱学校全部进行改造.根据预算,共需资金1575万元.改造一所A类学校和两所B类学校共需资金230万元;改造两所A类学校和一所B类学校共需资金205万元.
(1)改造一所A类学校和一所B类学校所需的资金分别是多少万元?
(2)若该县的A类学校不超过5所,则B类学校至少有多少所?
(3)我市计划今年对该县A、B两类学校共6所进行改造,改造资金由国家财政和地方财政共同承担.若今年国家财政拨付的改造资金不超过400万元;地方财政投入的改造资金不少于70万元,其中地方财政投入到A、B两类学校的改造资金分别为每所10万元和15万元.请你通过计算求出有几种改造方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求一个正数的算术平方根,有些数可以直接求得,如 ![]() ,有些数则不能直接求得,如
,有些数则不能直接求得,如 ![]() .但可以利用计算器求得,还可以通过一组数的内在联系,运用规律求得. 请同学们观察下表:
.但可以利用计算器求得,还可以通过一组数的内在联系,运用规律求得. 请同学们观察下表:
n | 0.09 | 9 | 900 | 90000 | … |
| 0.3 | 3 | 30 | 300 | … |
运用你发现的规律解决问题,已知 ![]() ≈1.435,则
≈1.435,则 ![]() ≈( )
≈( )
A.14.35
B.1.435
C.0.1435
D.143.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com