
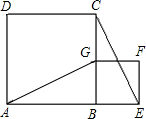
 如图,正方形BEFG的边BG在正方形ABCD的边BC上,连结AG,EC.
如图,正方形BEFG的边BG在正方形ABCD的边BC上,连结AG,EC.分析 (1)先利用正方形的性质得到BA=BC,∠ABC=90°,BG=BE,∠GBE=90°,然后根据“SAS”判断△ABG≌△CBE,从而得到AG=CE;
(2)利用旋转的定义,可把△ABG绕点B顺时针旋转90°得到△CBE;
(3)利用△ABG≌△CBE得到∠BAG=∠BCE,然后根据三角形内角和定理得到∠ABG=∠CMG=90°,于是可判定AM⊥CE.
解答 解:(1)∵四边形ABCD和四边形BEFG都为正方形,
∴BA=BC,∠ABC=90°,BG=BE,∠GBE=90°,
在△ABG和△CBE中
$\left\{\begin{array}{l}{AB=CB}\\{∠ABG=∠CBE}\\{BG=BE}\end{array}\right.$,
∴△ABG≌△CBE,
∴AG=CE;
(2)存在.
把△ABG绕点B顺时针旋转90°可得到△CBE;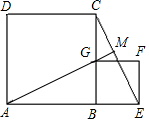
(3)AM⊥CE.
理由如下:
∵△ABG≌△CBE,
∴∠BAG=∠BCE,
∵∠AGB=∠CGM,
∴∠ABG=∠CMG=90°,
∴AM⊥CE.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了正方形的性质.


科目:初中数学 来源: 题型:解答题
 某校1200名学生参加了全市得到“读数”活动,该校随机选取部分学生,对他们在三、四两个月的读数时间进行调查,并根据调查数据制作统计表和如图所示的频数分布直方图,均不完整,解答下列问题.
某校1200名学生参加了全市得到“读数”活动,该校随机选取部分学生,对他们在三、四两个月的读数时间进行调查,并根据调查数据制作统计表和如图所示的频数分布直方图,均不完整,解答下列问题.| 日人均读书时间x/h | 人数/人 | 百分比 |
| 0≤x≤0.5 | 6 | |
| 0.5<x≤1 | 30 | |
| 1<x≤1.5 | 50% | |
| 1.5<x≤2 | 10 | 10% |
| 2<x≤2.5 | b | c |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进20海里到达B点,此时,测得海岛C位于北偏东45°的方向,请求出海岛C到航线AB的距离(结果保留根号).
如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进20海里到达B点,此时,测得海岛C位于北偏东45°的方向,请求出海岛C到航线AB的距离(结果保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
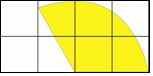 在如图所示的网格中,每个小正方形的边长都为1,若以小正形的顶点为圆心,2为半径作一个扇形围成一个圆锥,则所围成的圆锥的底面圆的半径为$\frac{2}{3}$.
在如图所示的网格中,每个小正方形的边长都为1,若以小正形的顶点为圆心,2为半径作一个扇形围成一个圆锥,则所围成的圆锥的底面圆的半径为$\frac{2}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
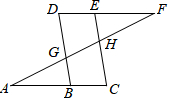 如图,点E在直线DF上,点B在直线AC上,若∠AGB=∠EHF,∠C=∠D,则∠A与∠F的大小关系是( )
如图,点E在直线DF上,点B在直线AC上,若∠AGB=∠EHF,∠C=∠D,则∠A与∠F的大小关系是( )| A. | ∠A+∠F=90° | B. | ∠A>∠F | C. | ∠A<∠F | D. | ∠A=∠F |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3.1415926 | B. | $\frac{22}{7}$ | C. | π | D. | $\sqrt{36}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com