
【题目】某学校为增加体育馆观众坐席数量,决定对体育馆进行施工改造.如图,为体育馆改造的截面示意图.已知原座位区最高点A到地面的铅直高度AC长度为15米,原坡面AB的倾斜角∠ABC为45°,原坡脚B与场馆中央的运动区边界的安全距离BD为5米.如果按照施工方提供的设计方案施工,新座位区最高点E到地面的铅直高度EG长度保持15米不变,使A、E两点间距离为2米,使改造后坡面EF的倾斜角∠EFG为37°.若学校要求新坡脚F需与场馆中央的运动区边界的安全距离FD至少保持2.5米(即FD≥2.5),请问施工方提供的设计方案是否满足安全要求呢?请说明理由.(参考数据:sin37°≈![]() ,tan37°≈
,tan37°≈![]() )
)

【答案】施工方提供的设计方案不满足安全要求.
【解析】试题分析:
在Rt△ABC中,由∠ACB=90°,AC=15m,∠ABC=45°可求得BC=15m;在Rt△EGD中,由∠EGD=90°,EG=15m,∠EFG=37°,可解得GF=20m;通过已知条件可证得四边形EACG是矩形,从而可得GC=AE=2m;这样可解得:DF=GC+BC+BD-GF=2+15+5-20=2<2.5,由此可知:“设计方案不满足安全要求”.
试题解析:
施工方提供的设计方案不满足安全要求,理由如下:
在Rt△ABC中,AC=15m,∠ABC=45°,
∴BC=![]() =15m.
=15m.
在Rt△EFG中,EG=15m,∠EFG=37°,
∴GF=![]() ≈
≈![]() =20m.
=20m.
∵EG=AC=15m,AC⊥BC,EG⊥BC,
∴EG∥AC,
∴四边形EGCA是矩形,
∴GC=EA=2m,
∴DF=GC+BC+BD-GF=2+15+5-20=2<2.5.
∴施工方提供的设计方案不满足安全要求.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】对于三个数a、b、c,用Ma,b,c表示这三个数的中位数,用maxa,b,c表示这三个数中最大数,例如:M2,1,01,max2,1,00,max2,1,a![]() 解决问题:Msin45,cos60,tan60_____,如果max3,53x,2x63,则x的取值范围为______.
解决问题:Msin45,cos60,tan60_____,如果max3,53x,2x63,则x的取值范围为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx﹣16的图象经过点(﹣2,﹣40)和点(6,8).
(1)求这个二次函数图象与x轴的交点坐标;
(2)当y>0时,直接写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
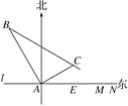
【题目】在某飞机场东西方向的地面l上有一长为1 km的飞机跑道MN(如图),在跑道MN的正西端14.5千米处有一观察站A.某时刻测得一架匀速直线降落的飞机位于点A的北偏西30°,且与点A相距15千米的B处;经过1分钟,又测得该飞机位于点A的北偏东60°,且与点A相距5![]() 千米的C处.
千米的C处.
(1)该飞机航行的速度是多少千米/小时?(结果保留根号)
(2)如果该飞机不改变航向继续航行,那么飞机能否降落在跑道MN之间?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
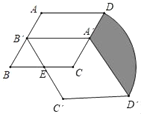
【题目】如图,在菱形ABCD中,∠B=60°,AB=2,把菱形ABCD绕BC的中点E顺时针旋转60°得到菱形A'B'C'D',其中点D的运动路径为![]() ,则图中阴影部分的面积为__.
,则图中阴影部分的面积为__.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农科所研究出一种新型的花生摘果设备,一期研发成本为每台6万元,该摘果机的销售量![]() (台)与售价
(台)与售价![]() (万元/台)之间存在函数关系:
(万元/台)之间存在函数关系:![]() .
.
(1)设这种摘果机一期销售的利润为![]() (万元),问一期销售时,在抢占市场份额(提示:销量尽可能大)的前提下利润达到32万元,此时售价为多少?
(万元),问一期销售时,在抢占市场份额(提示:销量尽可能大)的前提下利润达到32万元,此时售价为多少?
(2)由于环保局要求该机器必须增加除尘设备,科研所投入了7万元研究经费,使得环保达标且机器的研发成本每台降低了1万元,若科研所的销售战略保持不变,请问在二期销售中利润达到63万元时,该机器单台的售价为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=1,下列结论:①2a+b=0;②9a+c>3b;③若点A(﹣3,y1)、点B(﹣![]() ,y2)、点C(
,y2)、点C(![]() ,y3)在该函数图象上,则y1<y3<y2:④若方程ax2+bx+c=﹣3(a≠0)的两根为x1和x2,且x1<x2,则x1<﹣1<3<x2;⑤m(am+b)﹣b<a.其中正确的结论有( )
,y3)在该函数图象上,则y1<y3<y2:④若方程ax2+bx+c=﹣3(a≠0)的两根为x1和x2,且x1<x2,则x1<﹣1<3<x2;⑤m(am+b)﹣b<a.其中正确的结论有( )
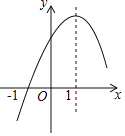
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中点A的坐标为(3,6),点B(6,0),C是线段OB上一动点(不与O,B重合),过C,O两点的二次函数y1和过C,B两点的二次函数y2的图像开口均向下,它们的顶点分别为OA,AB边上的E,F两点,点C从点O到点B运动过程中,阴影部分的面积大小变化情况是( )
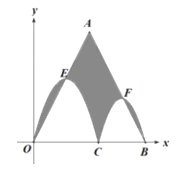
A.不变B.先增大再减小C.先减小再增大D.无法确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com