
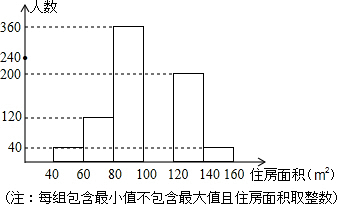
 某市春季房交会期间,某公司对参加本次房交会的消费者进行了随机的问卷调查,共发放1000份调查问卷,并全部收回,根据调查问卷,将消费者年收入的情况整理后,制成表格如下,将消费者打算购买住房面积的情况整理后,作出部频数分布直方图如图:
某市春季房交会期间,某公司对参加本次房交会的消费者进行了随机的问卷调查,共发放1000份调查问卷,并全部收回,根据调查问卷,将消费者年收入的情况整理后,制成表格如下,将消费者打算购买住房面积的情况整理后,作出部频数分布直方图如图:| 年收入(万元) | 1.2 | 1.8 | 3.0 | 5.0 | 10.0 |
| 被调查的消费者数(人) | 200 | 300 | 400 | 70 | 30 |
分析 (1)利用判断即可;
(2)根据总人数求出打算购买100-120平方米住房的人数,画出条形图即可;
(3)根据条形图,百分比的意义计算即可;
解答 解:(1)被调查的消费者平均年收入=$\frac{1.2×200+1.8×300+3.0×400+5.0×70+10.0×30}{200+300+400+70+30}$=2.63;
被调查的消费者年收入的中位数是=$\frac{1.8+3.0}{2}$=2.4;
众数是3.0;
故答案分别为2.63,2.4,3.0.
(2)补全分布直方图如图所示,
(3)打算购买100-120平方米住房的人数为240人;
打算购买住房面积小于100平方米的消费者人数占被调查消费者人数的百分数为$\frac{520}{1000}$=52%.
点评 本题考查频数分布直方图、加权平均数公式计算、中位数、众数的定义等知识,解题的关键是熟练掌握基本概念,灵活运用所学知识解决问题.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com