
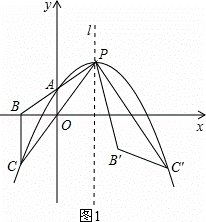
如图,抛物线y=a(x﹣m)2+2m﹣2(其中m>1)与其对称轴l相交于点P,与y轴相交于点A(0,m﹣1).连接并延长PA、PO,与x轴、抛物线分别相交于点B、C,连接BC.点C关于直线l的对称点为C′,连接PC′,即有PC′=PC.将△PBC绕点P逆时针旋转,使点C与点C′重合,得到△PB′C′.
(1)该抛物线的解析式为 (用含m的式子表示);
(2)求证:BC∥y轴;
(3)若点B′恰好落在线段BC′上,求此时m的值.
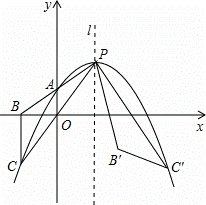
(1)解:∵A(0,m﹣1)在抛物线y=a(x﹣m)2+2m﹣2上,
∴a(0﹣m)2+2m﹣2=m﹣1.
∴a=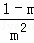 .
.
∴抛物线的解析式为y=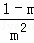 (x﹣m)2+2m﹣2.
(x﹣m)2+2m﹣2.
(2)证明:如图1,
设直线PA的解析式为y=kx+b,
∵点P(m,2m﹣2),点A(0,m﹣1).
∴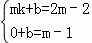 .
.
解得: .
.
∴直线PA的解析式是y=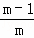 x+m﹣1.
x+m﹣1.
当y=0时,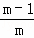 x+m﹣1=0.
x+m﹣1=0.
∵m>1,
∴x=﹣m.
∴点B的横坐标是﹣m.
设直线OP的解析式为y=k′x,
∵点P的坐标为(m,2m﹣2),
∴k′m=2m﹣2.
∴k′= .
.
∴直线OP的解析式是y= x.
x.
联立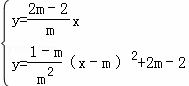
解得: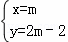 或
或 .
.
∵点C在第三象限,且m>1,
∴点C的横坐标是﹣m.
∴BC∥y轴.
(3)解:若点B′恰好落在线段BC′上,
设对称轴l与x轴的交点为D,连接CC′,如图2,
则有∠PB'C'+∠PB'B=180°.
∵△PB′C′是由△PBC绕点P逆时针旋转所得,
∴∠PBC=∠PB'C',PB=PB′,∠BPB′=∠CPC′.
∴∠PBC+∠PB'B=180°.
∵BC∥AO,
∴∠ABC+∠BAO=180°.
∴∠PB'B=∠BAO.
∵PB=PB′,PC=PC′,
∴∠PB′B=∠PBB′= ,
,
∴∠PCC′=∠PC′C=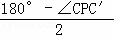 .
.
∴∠PB′B=∠PCC′.
∴∠BAO=∠PCC′.
∵点C关于直线l的对称点为C′,
∴CC′⊥l.
∵OD⊥l,
∴OD∥CC′.
∴∠POD=∠PCC′.
∴∠POD=∠BAO.
∵∠AOB=∠ODP=90°,∠POD=∠BAO,
∴△BAO∽△POD.
∴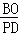 =
= .
.
∵BO=m,PD=2m﹣2,AO=m﹣1,OD=m,
∴ =
=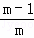
 .
.
解得:
∴m1=2+ ,m2=2﹣
,m2=2﹣ .
.
经检验:m1=2+ ,m2=2﹣
,m2=2﹣ 都是分式方程的解.
都是分式方程的解.
∵m>1,
∴m=2+ .
.
∴若点B′恰好落在线段BC′上,此时m的值为2+ .
.



科目:初中数学 来源: 题型:
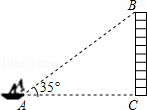
如图,从一般船的点A处观测海岸上高为41m的灯塔BC(观测点A与灯塔底部C在一个水平面上),测得灯塔顶部B的仰角为35°,则观测点A到灯塔BC的距离约为 m(精确到1m).
(参考数据:sin35°≈0.6,cos35°≈0.8,tan35°≈0.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
某工厂一种产品2013年的产量是100万件,计划2015年产量达到121万件.假设2013年到2015年这种产品产量的年增长率相同.
(1)求2013年到2015年这种产品产量的年增长率;
(2)2014年这种产品的产量应达到多少万件?
查看答案和解析>>
科目:初中数学 来源: 题型:
在班级组织的“贵阳市创建国家环保模范城市”知识竞赛中,小悦所在小组8名同学的成绩分别为(单位:分)95,94,94,98,94,90,94,90,则这8名同学成绩的众数是( )
|
| A. | 98分 | B. | 95分 | C. | 94分 | D. | 90分 |
查看答案和解析>>
科目:初中数学 来源: 题型:
“六•一”期间,小洁的妈妈经营的玩具店进了一纸箱除颜色外都相同的散装塑料球共1000个,小洁将纸箱里面的球搅匀后,从中随机摸出一个球记下其颜色,把它放回纸箱中;搅匀后再随机摸出一个球记下其颜色,把它放回纸箱中;…多次重复上述过程后,发现摸到红球的频率逐渐稳定在0.2,由此可以估计纸箱内红球的个数约是 个.
查看答案和解析>>
科目:初中数学 来源: 题型:
某校为了解该校九年级学生对蓝球、乒乓球、羽毛球、足球四种球类运动项目的喜爱情况,对九年级部分学生进行了随机抽样调查,每名学生必须且只能选择最喜爱的一项运动项目上,将调查结果统计后绘制成如图两幅不完整的统计图,请根据图中的信息,回答下列问题:
(1)这次被抽查的学生有 ”对应扇形的圆心角是 度;
(3)若该校九年级共有480名学生,估计该校九年级最喜欢足球的学生约有 人.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com