
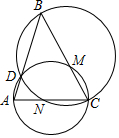 如图,在锐角△ABC中,∠ACB=60°,点D为线段AB上的一点,△ACD的外接圆交BC于点M,△BCD的外接圆交AC于点N,则$\frac{CM}{CA}$+$\frac{CN}{CB}$=( )
如图,在锐角△ABC中,∠ACB=60°,点D为线段AB上的一点,△ACD的外接圆交BC于点M,△BCD的外接圆交AC于点N,则$\frac{CM}{CA}$+$\frac{CN}{CB}$=( )| A. | 1 | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
分析 如图,连接BN、DM,延长DM交圆于F,连接BF、FN、FC,在CB上取一点P,使得CN=CP,连接PN.首先证明△BNF是等边三角形,再证明△BNP≌△FNC,推出BP=CF,推出BC=BP+PC=CF+CN,由△ACB∽△MCF,可得$\frac{CM}{AC}$=$\frac{CF}{BC}$,推出$\frac{CM}{CA}$+$\frac{CN}{CB}$=$\frac{CF}{BC}$+$\frac{CN}{BC}$=$\frac{CF+CN}{BC}$=$\frac{BC}{BC}$=1,即可解决问题.
解答 解:如图,连接BN、DM,延长DM交圆于F,连接BF、FN、FC,在CB上取一点P,使得CN=CP,连接PN.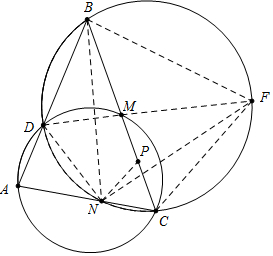
∵∠BDM=∠ACB=60°,∠ADN=∠ACB=60°(圆内接四边形的外角等于内对角),
∴∠BNF=∠BDF=∠BCF=60°,∠BFN=∠ACB=60°,
∴△BNF是等边三角形,
∵CN=CP,∠NCP=60°,
∴△NCP是等边三角形,
∴NB=NF,NP=NC,∠BNF=∠PNC,
∴∠BNP=∠FNC,
∴△BNP≌△FNC,
∴BP=CF,
∴BC=BP+PC=CF+CN,
∵∠ABC=∠CFM,∠ACB=∠FCM,
∴△ACB∽△MCF,
∴$\frac{CM}{AC}$=$\frac{CF}{BC}$,
∴$\frac{CM}{CA}$+$\frac{CN}{CB}$=$\frac{CF}{BC}$+$\frac{CN}{BC}$=$\frac{CF+CN}{BC}$=$\frac{BC}{BC}$=1,
故选A.
点评 本题考查三角形的外接圆与外心、全等三角形的判定和性质、相似三角形的判定和性质、等边三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会用转化的思想思考问题,属于中考压选择题中的压轴题.


科目:初中数学 来源: 题型:填空题
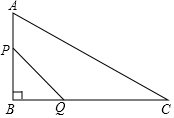 如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB匀速移动到点B,动点Q从点B开始沿边BC匀速移动到点B,如果P、Q两点分别从A、B两点同时出发,同时到达终点,则线段PQ的中点的运动路径长为6$\sqrt{5}$mm.
如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB匀速移动到点B,动点Q从点B开始沿边BC匀速移动到点B,如果P、Q两点分别从A、B两点同时出发,同时到达终点,则线段PQ的中点的运动路径长为6$\sqrt{5}$mm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
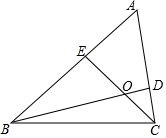 如图,D、E分别为△ABC的AC、AB边上的点,BD、CE相交于点O,若S△DOC=2,S△BOE=3,S△BOC=6,则S四边形AEOD=3.4.
如图,D、E分别为△ABC的AC、AB边上的点,BD、CE相交于点O,若S△DOC=2,S△BOE=3,S△BOC=6,则S四边形AEOD=3.4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
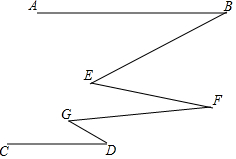 如图,AB∥CD,∠E=∠G=30°,则下列判断中正确的是( )
如图,AB∥CD,∠E=∠G=30°,则下列判断中正确的是( )| A. | ∠D=∠F=∠B | B. | ∠B+∠F+∠D=60° | C. | ∠B+∠F+∠D=120° | D. | GD∥EF |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ∵(2x-2)(3x-4)=0,∴2x-2=0或3x-4=0 | B. | ∵(x+3)(x-1)=1,∴x+3=0或x-1=1 | ||
| C. | ∵(x-2)(x-3)=2×3,∴x-2=2或x-3=3 | D. | ∵x(x+2)=0,∴x+2=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com