
【题目】如图1,等边△ABC边长为6,AD是△ABC的中线,P为线段AD(不包括端点A、D)上一动点,以CP为一边且在CP左下方作如图所示的等边△CPE,连结BE.
(1)点P在运动过程中,线段BE与AP始终相等吗?说说你的理由;
(2)若延长BE至F,使得CF=CE=5,如图2,问:求出此时AP的长;
(3)当点P在线段AD的延长线上时,F为线段BE上一点,使得CF=CE=5.求EF的长
【答案】
(1)
解:BE=AP;理由如下:
∵△ABC和△CPE均为等边三角形,
∴∠ACB=∠PCE=60°,AC=BC,CP=CE.
∵∠ACP+∠DCP=∠DCE+∠PCD=60°,
∴∠ACP=∠BCE.
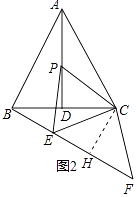
∵在△ACP和△BCE中, 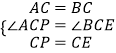 ,
,
∴△ACP≌△BCE(SAS).
∴BE=AP
(2)
解:如图2所示:过点C作CH⊥BE,垂足为H.∵AB=AC,AD是BC的中点,
∴∠CAD=∠BAD= ![]() ∠BAC=30°.
∠BAC=30°.
∵由(1)可知:△ACP≌△BCE,
∴∠CBE=∠CAD=30°,AP=BE.
∵在Rt△BCH中,∠HBC=30°,
∴HC= ![]() BC=3,BH=
BC=3,BH= ![]() BC=3
BC=3 ![]() .
.
∵在Rt△CEH中,EC=5,CH=3,
∴EH= ![]() =
= ![]() =4.
=4.
∴BE=HB﹣EH=3 ![]() ﹣4.
﹣4.
∴AP=3 ![]() ﹣4
﹣4
(3)
解:如图3所示:过点C作CH⊥BE,垂足为H.
∵△ABC和△CEP均为等边三角形,
∴AC=BC,CE=PC,∠ACB=∠ECP.
∴∠ACB+∠BCP=∠ECP+BCP,即∠BCE=∠ACP.
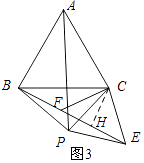
∵在△ACP和△BCE中, 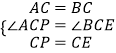 ,
,
∴△ACP≌△BCE(SAS).
∴∠CBH=∠CAP=30°.
∵在Rt△BCH中,∠CBH=30°,
∴HC= ![]() BC=3.
BC=3.
∵FC=CE,CH⊥FE,
∴FH=EH.
∴FH=EH= ![]() =
= ![]() =4.
=4.
∴EF=FH+EH=4+4=8.
【解析】(1)证出∠ACP=∠BCE.由SAS证明△ACP≌△BCE,得出对应边相等即可.(2)过点C作CH⊥BE,垂足为H.由等边三角形的性质得出∠CAD=∠BAD= ![]() ∠BAC=30°.由(1)可知:△ACP≌△BCE,得出∠CBE=∠CAD=30°,AP=BE.由含30°角的直角三角形的性质得出HC=
∠BAC=30°.由(1)可知:△ACP≌△BCE,得出∠CBE=∠CAD=30°,AP=BE.由含30°角的直角三角形的性质得出HC= ![]() BC=3,由勾股定理得出BH=
BC=3,由勾股定理得出BH= ![]() BC=3
BC=3 ![]() .在Rt△CEH中,由勾股定理求出EH=
.在Rt△CEH中,由勾股定理求出EH= ![]() =4,即可得出AP的长.(3)过点C作CH⊥BE,垂足为H.由SAS证明△ACP≌△BCE,得出∠CBH=∠CAP=30°.由含30°角的直角三角形的性质得出HC=
=4,即可得出AP的长.(3)过点C作CH⊥BE,垂足为H.由SAS证明△ACP≌△BCE,得出∠CBH=∠CAP=30°.由含30°角的直角三角形的性质得出HC= ![]() BC=3.与等腰三角形的性质求出FH=EH.由勾股定理求出FH,即可得出EF的长.
BC=3.与等腰三角形的性质求出FH=EH.由勾股定理求出FH,即可得出EF的长.
【考点精析】认真审题,首先需要了解全等三角形的性质(全等三角形的对应边相等; 全等三角形的对应角相等).


科目:初中数学 来源: 题型:
【题目】随着人们生活质量的提高,净水器已经慢慢走入了普通百姓家庭,某电器公司销售每台进价分别为2000元、1700元的A、B两种型号的净水器,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 18000元 |
第二周 | 4台 | 10台 | 31000元 |
(1)求A,B两种型号的净水器的销售单价;
(2)若电器公司准备用不多于54000元的金额在采购这两种型号的净水器共30台,求A种型号的净水器最多能采购多少台?
(3)在(2)的条件下,公司销售完这30台净水器能否实现利润为12800元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足,下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=EF=EC;④BA+BC=2BF,其中正确的结论有(填序号). 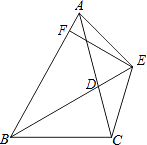
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁四位选手各10次射击成绩的方差如下表:
选手 | 甲 | 乙 | 丙 | 丁 |
方差(环2) | 0.035 | 0.015 | 0.025 | 0.027 |
则这四人中成绩发挥最稳定的是( )
A. 甲 B. 乙 C. 丙 D. 丁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm,P、Q是△ABC边上的两个动点,其 中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒. 
(1)当t=2秒时,求PQ的长;
(2)求出发时间为几秒时,△PQB是等腰三角形?
(3)若Q沿B→C→A方向运动,则当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】油桶制造厂的某车间主要负责生产制造油桶用的的圆形铁片和长方形铁片,该车间有工人42人,每个工人平均每小时可以生产圆形铁片120片或者长方形铁片80片.如图,一个油桶由两个圆形铁片和一个长方形铁片相配套. 生产圆形铁片和长方形铁片的工人各为多少人时,才能使生产的铁片恰好配套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△A1B1C1是△ABC向右平移四个单位长度后得到的,且三个顶点的坐标分别为A1(1,1),B1(4,2),C1(3,4).
(1)请画出△ABC,并写出点A、B、C的坐标;
(2)求出△AOA1的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com