
【题目】将一副三角板Rt△ABD与Rt△ACB(其中∠ABD=∠ACB=90°,∠D=60°,∠ABC=45°)如图摆放,Rt△ABD中∠D所对的直角边与Rt△ACB的斜边恰好重合.以AB为直径的圆经过点C,且与AD相交于点E,连接EB,连接CE并延长交BD于F.
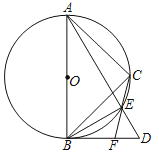
(1)求证:EF平分∠BED;
(2)求△BEF与△DEF的面积的比值.
科目:初中数学 来源: 题型:
【题目】端午节当天,小明带了四个粽子(除味道不同外,其它均相同),其中两个是大枣味的,另外两个是火腿味的,准备按数量平均分给小红和小刚两个好朋友.
(1)请你用树状图或列表的方法表示小红拿到的两个粽子的所有可能性;
(2)请你计算小红拿到的两个粽子刚好是同一味道的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
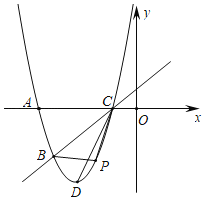
【题目】如图,已知抛物线![]() 经过
经过![]() ,
,![]() 两点,与x轴的另一个交点为C,顶点为D,连结CD.
两点,与x轴的另一个交点为C,顶点为D,连结CD.
(1)求该抛物线的表达式;
(2)点P为该抛物线上一动点(与点B、C不重合),设点P的横坐标为t.
①当点P在直线BC的下方运动时,求![]() 的面积的最大值;
的面积的最大值;
②该抛物线上是否存在点P,使得![]() 若存在,求出所有点P的坐标;若不存在,请说明理由.
若存在,求出所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
情境观察:将矩形ABCD纸片沿对角线AC剪开,得到△ABC和△A′C′D,如图1所示.将△A′C′D的顶点A′与点A重合,并绕点A按逆时针方向旋转,使点D、A(A′)、B在同一条直线上,如图2所示.
观察图2可知:与BC相等的线段是 ▲ ,∠CAC′= ▲ °.
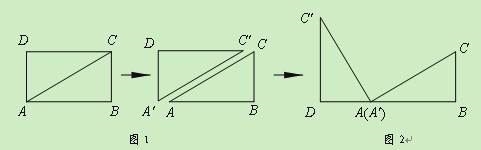
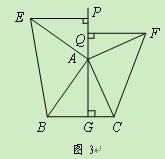
问题探究:如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q. 试探究EP与FQ之间的数量关系,并证明你的结论.
拓展延伸:如图4,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF,射线GA交EF于点H. 若AB=k AE,AC=k AF,试探究HE与HF之间的数量关系,并说明理由.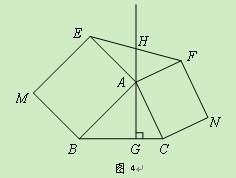
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AC=n+1(其中n为正整数),点B在线段AC上,在线段AC同侧作菱形ABMN与菱形BCEF,点F在BM边上,AB=n,∠ABM=60°,连接AM、ME、EA得到△AME.当AB=1时,△AME的面积记为S1;当AB=2时,△AME的面积记为S2;当AB=3时,△AME的面积记为S3;…;当AB=n时,△AME的面积记为Sn,当n≥2时,Sn﹣Sn﹣1=__.

查看答案和解析>>
科目:初中数学 来源: 题型:
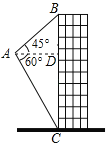
【题目】如图,航模小组用无人机来测量建筑物BC的高度,无人机从A处测得建筑物顶部B的仰角为45°,测得底部C的俯角为60°,若此时无人机与该建筑物的水平距离AD为30m,则该建筑物的高度BC为_____m.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy中,对于点A和线段BC,给出如下定义:若△ABC是等腰直角三角形,则称点A为BC的“等直点”;特别的,若△ABC是以BC为斜边的等腰直角三角形,则称点A为BC的“完美等直点”.
(1)若B(﹣2,0),C(2,0),则在D(0,2),E(4,4),F(﹣2,﹣4),G(0,![]() )中,线段BC的“等直点”是 ;
)中,线段BC的“等直点”是 ;
(2)已知B(0,﹣6),C(8,0).
①若双曲线y=![]() 上存在点A,使得点A为BC的“完美等直点”,求k的值;
上存在点A,使得点A为BC的“完美等直点”,求k的值;
②在直线y=x+6上是否存在点P,使得点P为BC的“等直点”?若存在,求出点P的坐标;若不存在,请说明理由;
(3)若B(0,2),C(2,0),⊙T的半径为3,圆心为T(t,0).当在⊙T内部,恰有三个点是线段BC的“等直点”时,直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),与y轴的交点在(0,2),(0,3)之间(包含端点),顶点坐标为(1,n),则下列结论:
①2a+b<0;
②﹣1≤a≤﹣![]() ;
;
③对于任意实数m,a(m2﹣1)+b(m﹣1)≤0总成立;
④关于x的方程ax2+bx+c=n+1有两个不相等的实数根.
其中结论正确的序号是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com