
����Ŀ����һ�������ĺ����װ���ĸ��ֱ�������֩�1����2����3����4��С�����ǵ���״����С���ʵص���ȫ��ͬ��Сǿ�ȴӺ��������ȡ��һ��С��������Ϊx���Żغ���ҡ�Ⱥ�����С�����ȡ��һ��С��������Ϊy��
��1�����б�������״ͼ��ʾ����x��y�������п��ܳ��ֵĽ����
��2����Сǿ��С����ȡһ��С����ȷ���ĵ㣨x��y������һ�κ���y=x��1ͼ���ϵĸ��ʣ�
���𰸡�
��1��
�⣺�б��ã�
y x | ��1 | ��2 | ��3 | ��4 |
��1 | ����1����1�� | ����1����2�� | ����1����3�� | ����1����4�� |
��2 | ����2����1�� | ����2����2�� | ����2����3�� | ����2����4�� |
��3 | ����3����1�� | ����3����2�� | ����3����3�� | ����3����4�� |
��4 | ����4����1�� | ����4����2�� | ����4����3�� | ����4����4�� |
����16�ֵȿ��ܵĽ��
��2��
�⣺��Сǿ��С����ȡһ��С����ȷ���ĵ㣨x��y������һ�κ���y=x��1��ͼ���ϵ��У�����1����2��������2����3��������3����4����
��Сǿ��С����ȡһ��С����ȷ���ĵ㣨x��y������һ�κ���y=x��1��ͼ���ϵĸ���Ϊ�� ![]()
����������1�����ȸ������⻭������Ȼ������״ͼ������еȿ��ܵĽ������2���ɣ�1���е���״ͼ���������Сǿ��С����ȡһ��С����ȷ���ĵ㣨x��y������һ�κ���y=x��1��ͼ���ϵ�����������ø��ʹ�ʽ������ô𰸣�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���
��1����̽�����֡���ͼ�٣���һ��ֱ��������ֽƬ����B=60�㣬С������м���һ���ԡ�BΪ�ڽ���������ľ��Σ�������β������֣���������λ��DE��EF����ʱ�����õľ��ε������������ͨ��֤����֤������ȷ�ԣ����ó������ε���������ԭ����������ı�ֵΪ ��
��2������չӦ�á���ͼ�ڣ��ڡ�ABC�У�BC=a��BC���ϵĸ�AD=h������PQMN�Ķ���P��N�ֱ��ڱ�AB��AC�ϣ�����Q��M�ڱ�BC�ϣ������PQMN��������ֵΪ �� ���ú�a��h�Ĵ���ʽ��ʾ��
��3�������Ӧ�á���ͼ�ۣ���һ�顰ȱ�Ǿ��Ρ�ABCDE��AB=32��BC=40��AE=20��CD=16��С�����м�����һ��������ľ��Σ���BΪ���������ε��ڽǣ�����þ��ε������
��4����ʵ��Ӧ�á���ͼ�ܣ�����һ���ı��ε�ľ������ABCD��������AB=50cm��BC=108cm��CD=60cm����tanB=tanC= ![]() ��ľ����ʦ������������вó��˶���M��N�ڱ�BC����������ľ���PQMN����þ��ε������
��ľ����ʦ������������вó��˶���M��N�ڱ�BC����������ľ���PQMN����þ��ε������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ�����ABC�У�AB=AC=4cm����B=30�㣬��P�ӵ�B�������� ![]() cm/s���ٶ���BC�����˶�����Cֹͣ��ͬʱ��Q�ӵ�B��������1cm/s���ٶ���BA��AC�����˶�����Cֹͣ������BPQ�����Ϊy��cm2�����˶�ʱ��Ϊx��s�������������ܷ�ӳy��x֮�亯����ϵ��ͼ���ǣ� ��
cm/s���ٶ���BC�����˶�����Cֹͣ��ͬʱ��Q�ӵ�B��������1cm/s���ٶ���BA��AC�����˶�����Cֹͣ������BPQ�����Ϊy��cm2�����˶�ʱ��Ϊx��s�������������ܷ�ӳy��x֮�亯����ϵ��ͼ���ǣ� ��
A.
B.
C.
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=ax2+bx+c��ͼ����ͼ��ʾ��������6������ʽ��ab��ac��a+b+c��2a+b��2a��b�У���ֵΪ����ʽ�ӵĸ����ǣ� �� 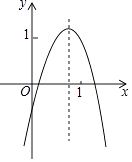
A.2��
B.3��
C.4��
D.5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ����CD�ǡ�O��һ���ң���CD��AB�ڵ�E��CD=4 ![]() ��AE=2�����O�İ뾶Ϊ ��
��AE=2�����O�İ뾶Ϊ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��˫����y= ![]() ��x��0����ֱ��EF���ڵ�A����B����AE=AB=BF������AO��BO�����Ƿֱ���˫����y=
��x��0����ֱ��EF���ڵ�A����B����AE=AB=BF������AO��BO�����Ƿֱ���˫����y= ![]() ��x��0�����ڵ�C����D����
��x��0�����ڵ�C����D����
��1����AB��CD��λ�ù�ϵ����
���ı���ABDC�����Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=3ax2+2bx+c
��1����a=b=1��c=��1�����������x��Ľ������ꣻ
��2����a= ![]() ��c=2+b���������ک�2��x��2�����ϵ���Сֵ�ǩ�3����b��ֵ��
��c=2+b���������ک�2��x��2�����ϵ���Сֵ�ǩ�3����b��ֵ��
��3����a+b+c=1���Ƿ����ʵ��x��ʹ����Ӧ��y��ֵΪ1����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ȱߡ�ABC�ı߳���2��D��E�ֱ�ΪAB��AC���е㣬�ӳ�BC����F��ʹCF= ![]() BC������CD��EF��
BC������CD��EF�� 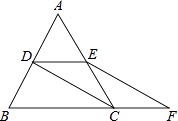
��1����֤��DE=CF��
��2����EF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1������ABCD�У���E��F�ֱ�ΪAB��AD���е㣬����CE��CF�� 
��1����֤��CE=CF��
��2����ͼ2����HΪAB��һ�㣬����CH��ʹ��CHB=2��ECB����֤��CH=AH+AB�� 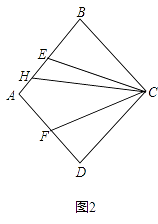
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com