
【题目】如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC交⊙O于点F. 
(1)AB与AC的大小有什么关系?为什么?
(2)若∠BAC=70°,求弧BD、弧DF和弧AF的度数.
【答案】
(1)解:AB=AC.
理由是:连接AD.
∵AB是⊙O的直径,
∴∠ADB=90°,即AD⊥BC,
又∵DC=BD,
∴AB=AC
(2)解:连接OD、OF.

∵△ABC中,AB=AC,∠BAC=70°,
∴∠ABC=∠C= ![]() =
= ![]() =55°,
=55°,
∵OB=OD,
∴∠ODB=∠OBD=55°,
∴∠BOD=180°﹣∠B﹣∠ODB=180°﹣55°﹣55°=70°,
∴ ![]() 的度数是70°;
的度数是70°;
同理,∠AOF=40°,
则∠DOF=180°﹣∠AOF﹣∠BOD=180°﹣40°﹣70°=70°.
则 ![]() 的度数是70°,
的度数是70°, ![]() 的度数是40°.
的度数是40°.
【解析】(1)连接AD,根据圆周角定理可以证得AD垂直且平分BC,然后根据垂直平分线的性质证得AB=AC;(2)连接OD、OF,利用等腰三角形的性质:等边对等角求得圆心角∠BOD、∠DOF、∠AOF的度数,根据弧的度数等于所对圆心角的度数即可求解.
【考点精析】通过灵活运用圆心角、弧、弦的关系和圆周角定理,掌握在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等;在同圆或等圆中,同弧等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半即可以解答此题.


科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,BD是△ABC的角平分线,P是射线AC上任意一点 (不与A、D、C三点重合),过点P作PQ⊥AB,垂足为Q,交线段BD于E.
(1)如图①,当点P在线段AC上时,说明∠PDE=∠PED.
(2)画出∠CPQ的角平分线交线段AB于点F,则PF与BD有怎样的位置关系?画出图形并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的方格纸中每个小方格都是边长为1个单位长度的正方形,在平面直角坐标系中,已知点A(0,-1),B(0,3),C(-3,2).
(1) 描出A、B、C三点的位置,并画出三角形ABC;
(2) 三角形ABC中任意一点P(x,y)平移后的对应点为P1(x+3,y-2)将三角形ABC作同样的平移得到三角形A1B1C1,作出平移后的图形,并写出点A1、B1、C1的坐标;
(3) 求三角形A1B1C1的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
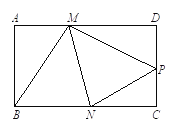
【题目】已知:如图,矩形纸片ABCD的边AD=3,CD=2,点P是边CD上的一个动点(不与点C重合,把这张矩形纸片折叠,使点B落在点P的位置上,折痕交边AD与点M,折痕交边BC于点N .
(1)写出图中的全等三角形. 设CP= ![]() ,AM=
,AM= ![]() ,写出
,写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)试判断∠BMP是否可能等于90°. 如果可能,请求出此时CP的长;如果不可能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市努力改善空气质量,近年来空气质量明显好转,根据该市环境保护局公布的2010﹣2014这五年各年全年空气质量优良的天数如表所示,根据表中信息回答:
2010 | 2011 | 2012 | 2013 | 2014 |
234 | 233 | 245 | 247 | 256 |
(1)这五年的全年空气质量优良天数的中位数是________,平均数是________;
(2)这五年的全年空气质量优良天数与它前一年相比增加最多的是________年(填写年份);
(3)求这五年的全年空气质量优良天数的方差________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将Rt△ABC(其中∠B=35°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C,A,B1在同一条直线上,那么旋转角等于( ) 
A.55°
B.70°
C.125°
D.145°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一天李小虎同学用“几何画板”画图,他先画了两条平行线AB,CD,然后在平行线间画了一点E,连接BE,DE后(如图①),他用鼠标左键点住点E,拖动后,分别得到如图②,③,④等图形,这时他突然一想,∠B,∠D与∠BED之间的度数有没有某种联系呢?接着小虎同学通过利用“几何画板”的“度量角度”和“计算”功能,找到了这三个角之间的关系.

(1)你能探究出图①到图④各图中的∠B,∠D与∠BED之间的关系吗?
(2)请从所得的四个关系中,选一个说明它成立的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com