
科目:初中数学 来源: 题型:解答题
 、
、 、
、 ,求这个三角形的面积.”小明同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图①所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.我们把上述求△ABC面积的方法叫做构图法.
,求这个三角形的面积.”小明同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图①所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.我们把上述求△ABC面积的方法叫做构图法.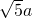 、
、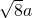 、
、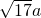 (a>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△DEF,并直接写出它的面积.
(a>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△DEF,并直接写出它的面积.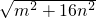 、
、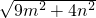 、
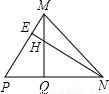
、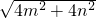 (m>0,n>0,且m≠n),试运用构图法求出△MNP的面积.
(m>0,n>0,且m≠n),试运用构图法求出△MNP的面积.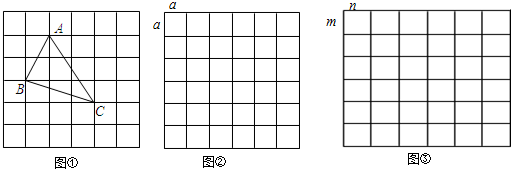
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com