
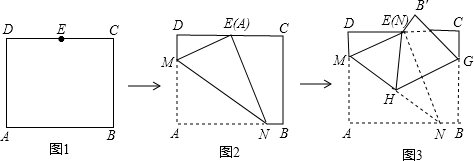
分析 如图2中,作NF⊥CD于F.设DM=x,则AM=EM=10-x,利用勾股定理求出x,再利用△DME∽△FEN,得$\frac{DE}{FN}$=$\frac{EM}{EN}$,求出EN,EM,求出tan∠AMN,再证明∠EHG=∠AMN即可解决问题.
解答 解: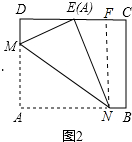 如图2中,作NF⊥CD于F.设DM=x,则AM=EM=10-x,
如图2中,作NF⊥CD于F.设DM=x,则AM=EM=10-x,
∵DE=EC,AB=CD=8$\sqrt{3}$,
∴DE=$\frac{1}{2}$CD=4$\sqrt{3}$,
在RT△DEM中,∵DM2+DE2=EM2,
∴(4$\sqrt{3}$)2+x2=(10-x)2,
解得x=2.6,
∴DM=2.6,AM=EM=7.4,
∵∠DEM+∠NEF=90°,∠NEF+∠ENF=90°,
∴∠DEM=∠ENF,∵∠D=∠EFN=90°,
∴△DME∽△FEN,
∴$\frac{DE}{FN}$=$\frac{EM}{EN}$,
∴$\frac{4\sqrt{3}}{10}$=$\frac{7.4}{EN}$,
∴EN=$\frac{37}{6}$$\sqrt{3}$,
∴AN=EN=$\frac{37}{6}$$\sqrt{3}$,
∴tan∠AMN=$\frac{AN}{AM}$=$\frac{5}{6}$$\sqrt{3}$,
如图3中,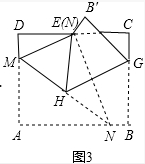 ∵ME⊥EN,HG⊥EN,
∵ME⊥EN,HG⊥EN,
∴EM∥GH,
∴∠NME=∠NHG,
∵∠NME=∠AMN,∠EHG=∠NHG,
∴∠AMN=∠EHG,
∴tan∠EHG=tan∠AMN=$\frac{5}{6}$$\sqrt{3}$.
方法二,tan∠EHG=tan∠EMN=$\frac{EN}{EM}$=$\frac{BC}{DE}$.
故答案为$\frac{5}{6}$$\sqrt{3}$.
点评 本题考查翻折变换、勾股定理、相似三角形的判定和性质等知识,解题的关键是学会把问题转化,证明∠AMN=∠EHG是关键,属于中考填空题中的压轴题.


 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x+$\frac{1}{y}$=2 | B. | xy+5=-4 | C. | 3x2+y=8 | D. | x+$\frac{y}{4}$=2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 等腰三角形ABC在平面直角坐标系中的位置如图所示,已知点A(-6,0),点B在原点,CA=CB=5,把等腰三角形ABC沿x轴正半轴作无滑动顺时针翻转,第一次翻转到位置①,第二次翻转到位置②…依此规律,第15次翻转后点C的横坐标是77.
等腰三角形ABC在平面直角坐标系中的位置如图所示,已知点A(-6,0),点B在原点,CA=CB=5,把等腰三角形ABC沿x轴正半轴作无滑动顺时针翻转,第一次翻转到位置①,第二次翻转到位置②…依此规律,第15次翻转后点C的横坐标是77.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0>a>b | B. | 0>b>a | C. | b>a>0 | D. | a>b>0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 有这样一个问题,探究函数y=$\frac{3}{x-2}$的图象和性质.小强根据学习一次函数的经验,对函数y=$\frac{3}{x-2}$的图象和性质进行了探究.
有这样一个问题,探究函数y=$\frac{3}{x-2}$的图象和性质.小强根据学习一次函数的经验,对函数y=$\frac{3}{x-2}$的图象和性质进行了探究.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com