
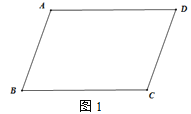
【题目】如图1,已知AD∥BC,∠B=∠D.
(1)求证:AB∥CD;
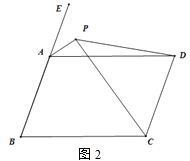
(2)如图2,点E为BA延长线上一点,∠EAD与∠BCD的角平分线交于点P.
①求∠APC的度数;
②连接DP,若∠PDC=750,则∠DPC-![]() ∠B=________.
∠B=________.
【答案】90°
【解析】
(1)根据平行线的性质和判定结合已知条件进行分析证明即可;
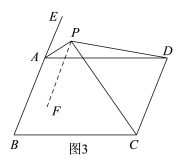
(2)①如图3,过点P作PF∥AB,结合已知条件易得∠EAP=∠APF,∠DCP=∠CPF,从而可得∠APC=∠EAP+∠DCP,由已知易得∠EAD=∠B,∠B+∠BCD=180°,进而可得∠EAD+∠BCD=180°,结合AP平分∠EAD,CP平分∠BCD即可得到∠APC=∠EAP+∠DCP=90°;②如图4,延长DP交BA的延长线于点M,由已知易得I、∠MPA+∠APF=75°,由∠APC=90°可得II、∠MPA+∠DPC=90°,再证∠APF=![]() ∠B,即可由I-II得到所求结果.
∠B,即可由I-II得到所求结果.
(1)∵AD∥BC,
∴∠ A+∠ B=180°,
∵∠ B=∠ D,即∠ A+∠ D =180°,
∴ AB∥CD;
(2)①过点P作直线PF∥AB,
∵在平行四边形ABCD中,AB∥CD,AD∥BC,
∴∠EAD=∠B,∠B+∠BCD=180°,AB∥PF∥CD,
∴∠EAD+∠BCD=180°,
∵AP平分∠EAD,CP平分∠BCD,
∴∠EAP=![]() ∠EAD,∠DCP=
∠EAD,∠DCP=![]() ∠BCD,
∠BCD,
∴∠EAP+∠DCP=![]() (∠EAD+∠BCD)=90°,
(∠EAD+∠BCD)=90°,
∵AB∥PF∥CD,
∴∠APF=∠EAP,∠CPF=∠DCP,
∴∠APC=∠APF+∠CPF=∠EAP+∠DCP=90°,即∠APC=90°;
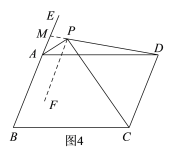
②如图4,延长DP交BA的延长线于点M,
∵AB∥PF∥CD,
∴∠APF=∠EAP=![]() ∠EAD=
∠EAD=![]() ∠B,∠MPA+∠APF=∠MPF=∠PDC=75°,
∠B,∠MPA+∠APF=∠MPF=∠PDC=75°,
∵∠APC=90°,
∴∠MPA+∠DPC=90°,
∴(∠MPA+∠DPC)-(∠MPA+∠APF)=90°-75°=15°,
∴∠DPC-∠APF=15°,
∴∠DPC-![]() ∠B=15°.
∠B=15°.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,点C是半圆O上一点,∠COB=60°,点D是OC的中点,连接BD,BD的延长线交半圆O于点E,连接OE,EC,BC. 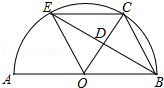
(1)求证:△BDO≌△EDC.
(2)若OB=6,则四边形OBCE的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线y=ax2+bx﹣2(a≠0)与x轴交于A(1,0),B(3,0)两点,与y轴交于点C,其顶点为点D,点E的坐标为(0,﹣1),该抛物线与BE交于另一点F,连接BC.
(1)求该抛物线的解析式;
(2)一动点M从点D出发,以每秒1个单位的速度沿与y轴平行的方向向上运动,连接OM,BM,设运动时间为t秒(t>0),在点M的运动过程中,当t为何值时,∠OMB=90°?
(3)在x轴上方的抛物线上,是否存在点P,使得∠PBF被BA平分?若存在,请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中, ![]() ,
, ![]() 为线段
为线段![]() 上一点,
上一点, ![]() ,
, ![]() 为射线
为射线![]() 上一点,且
上一点,且![]() ,连接
,连接![]() .
.
(![]() )如图
)如图![]() ,
,
①依题意补全图形.
②若![]() ,
, ![]() ,求
,求![]() 的长.
的长.
(![]() )如图
)如图![]() ,若
,若![]() ,连接
,连接![]() 并延长,交
并延长,交![]() 于点
于点![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某手机经销商计划同时购进一批甲、乙两种型号手机,若购进2部甲型号手机和5部乙型号手机,共需要资金6000元;若购进3部甲型手机和2部乙型手机,共需要资金4600元.
(1) 求甲、乙型号手机每部进价为多少元?
(2) 为了提高利润,该店计划购进甲、乙型号手机销售,预计用不多于1.84万元且不少于1.76万元的资金购进这两种手机共20部,请问有几种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,F为CD上一点,∠EFD=60°,∠AEC=2∠CEF,若6°<∠BAE<15°,∠C的度数为整数,则∠C的度数为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次男子马拉松长跑比赛中,随机抽得12名选手所用的时间(单位:分钟)得到如下样本数据:140 146 143 175 125 164 134 155 152 168 162 148
(1)计算该样本数据的中位数和平均数;
(2)如果一名选手的成绩是147分钟,请你依据样本数据的中位数,推断他的成绩如何?
查看答案和解析>>
科目:初中数学 来源: 题型:
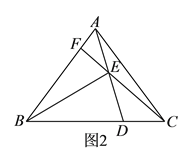
【题目】如图,在![]() 中,AD是
中,AD是![]() 的中线,过点A作
的中线,过点A作![]() 与AB的平行线DE交于点
与AB的平行线DE交于点![]() 与AC相交于点O,连接EC.
与AC相交于点O,连接EC.
![]() 求证:
求证: ![]() ;
;
![]() 当
当![]() 满足条件______时,四边形ADCE是菱形,请补充条件并证明.
满足条件______时,四边形ADCE是菱形,请补充条件并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,A(1,0)、点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为(﹣3,2).
(1)直接写出点E的坐标 ;
(2)在四边形ABCD中,点P从点B出发,沿“BC→CD”移动.若点P的速度为每秒1个单位长度,运动时间为t秒,回答下列问题:
①当t= 秒时,点P的横坐标与纵坐标互为相反数;
②求点P在运动过程中的坐标,(用含t的式子表示,写出过程);
③当3秒<t<5秒时,设∠CBP=x°,∠PAD=y°,∠BPA=z°,试问 x,y,z之间的数量关系能否确定?若能,请用含x,y的式子表示z,写出过程;若不能,说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com