
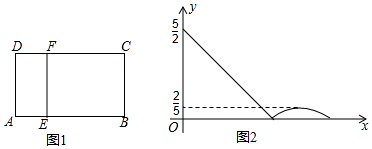
| A. | $\frac{23}{5}$ | B. | 5 | C. | 6 | D. | $\frac{25}{4}$ |
分析 易证△CFE∽△BEA,可得$\frac{CF}{BE}$=$\frac{CE}{AB}$,根据二次函数图象对称性可得E在BC中点时,CF有最大值,列出方程式即可解题.
解答 解:若点E在BC上时,如图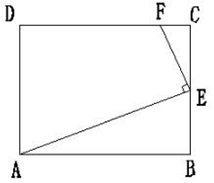
∵∠EFC+∠AEB=90°,∠FEC+∠EFC=90°,
∴∠CFE=∠AEB,∵在△CFE和△BEA中,$\left\{\begin{array}{l}{∠CFE=∠AEB}\\{∠C=∠B=90°}\end{array}\right.$,∴△CFE∽△BEA,
由二次函数图象对称性可得E在BC中点时,CF有最大值,此时$\frac{CF}{BE}$=$\frac{CE}{AB}$,BE=CE=x-$\frac{5}{2}$,即$\frac{y}{x-\frac{5}{2}}=\frac{x-\frac{5}{2}}{\frac{5}{2}}$,
∴y=${\frac{2}{5}(x-\frac{5}{2})}^{2}$,当y=$\frac{2}{5}$时,代入方程式解得:x1=$\frac{3}{2}$(舍去),x2=$\frac{7}{2}$,
∴BE=CE=1,∴BC=2,AB=$\frac{5}{2}$,
∴矩形ABCD的面积为2×$\frac{5}{2}$=5;
故选B.
点评 本题考查了二次函数顶点问题,考查了相似三角形的判定和性质,考查了矩形面积的计算,本题中由图象得出E为BC中点是解题的关键.


科目:初中数学 来源: 题型:选择题
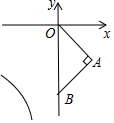 如图,平面直角坐标系中,等腰Rt△OAB沿x轴负方向向左平移后得到△O1A1B1,使点B的对应点B1落在双曲线y=$\frac{8}{x}$(x<0)上,若点B(0,-4),则线段AB扫过的面积是(平方单位)( )
如图,平面直角坐标系中,等腰Rt△OAB沿x轴负方向向左平移后得到△O1A1B1,使点B的对应点B1落在双曲线y=$\frac{8}{x}$(x<0)上,若点B(0,-4),则线段AB扫过的面积是(平方单位)( )| A. | 2 | B. | 2$\sqrt{2}$ | C. | 4 | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
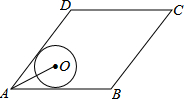 如图,菱形ABCD的边AB=20,面积为320,∠BAD<90°,⊙O与边AB,AD都相切,AO=10,则⊙O的半径长等于( )
如图,菱形ABCD的边AB=20,面积为320,∠BAD<90°,⊙O与边AB,AD都相切,AO=10,则⊙O的半径长等于( )| A. | 5 | B. | 6 | C. | 2$\sqrt{5}$ | D. | 3$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
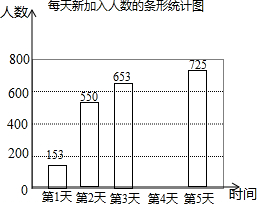 某数学学习网站为吸引更多人注册加入,举行了一个为期5天的推广活动,在活动期间,加入该网站的人数变化情况如下表所示:
某数学学习网站为吸引更多人注册加入,举行了一个为期5天的推广活动,在活动期间,加入该网站的人数变化情况如下表所示:| 时间 | 第1天 | 第2天 | 第3天 | 第4天 | 第5天 |
| 新加入人数(人) | 153 | 550 | 653 | b | 725 |
| 累计总人数(人) | 3353 | 3903 | a | 5156 | 5881 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
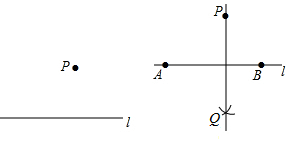
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com