
分析 (1)设购买一个A种商品需要x元,购买一个B种商品需要y元,根据等量关系:①购买一个A种商品比购买一个B种商品多用20元;②购买10个A种商品和5个B种商品共需275元;建立方程组求出其解即可;
(2)设该学校可购买z个A种商品,根据该学校本次购买A、B两种商品的总费用不超过1000元列出不等式,然后求解即可.
解答 解:(1)设购买一个A种商品需要x元,购买一个B种商品需要y元,依题意有
$\left\{\begin{array}{l}{x-y=20}\\{10x+5y=275}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=25}\\{y=5}\end{array}\right.$.
答:购买一个A种商品需要25元,购买一个B种商品需要5元.
(2)设该学校可购买z个A种商品,依题意有
80%×25z+5(3z+18)≤1000,
解得z≤26.
故该学校最多可购买26个A种商品.
点评 本题考查了二元一次方程组的运用,一元一次不等式组的运用,解决问题的关键是读懂题意,找到关键描述语,进而找到所求的量的数量关系.


科目:初中数学 来源: 题型:解答题
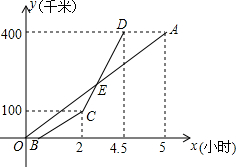 甲乙两地相距400千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地的路程y(千米)与所用时间x(小时)之间的函数关系,折线BCD表示轿车离甲地的路程y(千米)与x(小时)之间的函数关系,根据图象解答下列问题:
甲乙两地相距400千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地的路程y(千米)与所用时间x(小时)之间的函数关系,折线BCD表示轿车离甲地的路程y(千米)与x(小时)之间的函数关系,根据图象解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a-1<b-1 | B. | -3a>-2b | C. | a>b-16 | D. | $\frac{a}{5}<\frac{b}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解一批节能灯泡的使用寿命 | |
| B. | 了解某班同学“跳绳”的成绩 | |
| C. | 了解全国每天丢弃的塑料袋的数量 | |
| D. | 了解上海卫视“今晚80后”栏目的收视率 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
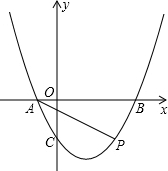 设抛物线$y=\frac{1}{2}{x}^{2}-\frac{3}{2}x-2$与x轴的交点为A(x1,0),B(x2,0),其中x1< x2,点P(m,n)为抛物线上一动点,连接AP,BP,当∠APB为锐角时,下列m的取值范围中正确的是①③⑤;(填序号)
设抛物线$y=\frac{1}{2}{x}^{2}-\frac{3}{2}x-2$与x轴的交点为A(x1,0),B(x2,0),其中x1< x2,点P(m,n)为抛物线上一动点,连接AP,BP,当∠APB为锐角时,下列m的取值范围中正确的是①③⑤;(填序号)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
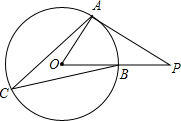 如图,PA为⊙O的切线,A为切点,B是OP与⊙O的交点,C是优弧AB上一点(不与点A、B重合).若∠P=36°,则∠ACB的大小为( )
如图,PA为⊙O的切线,A为切点,B是OP与⊙O的交点,C是优弧AB上一点(不与点A、B重合).若∠P=36°,则∠ACB的大小为( )| A. | 18° | B. | 27° | C. | 36° | D. | 54° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com