
����Ŀ����ͼ��������ABCD�У��Խ���AC��BD�ཻ�ڵ�O��AB=8����BAD=60�㣬��E�ӵ�A��������AB��ÿ��2����λ���ȵ��ٶ����յ�B�˶�������E�����A�غ�ʱ������E��EF��AD�ڵ�F����EG��AD��AC�ڵ�G������G��GH��AD��AD����AD���ӳ��ߣ��ڵ�H���õ�����EFHG�����E�˶���ʱ��Ϊt��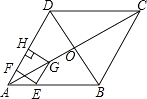
��1�����߶�EF�ij����ú�t�Ĵ���ʽ��ʾ����
��2�����H���D�غ�ʱt��ֵ��
��3�������EFHG������ABCD�ص�����ͼ�ε������Sƽ����λ����S��t֮��ĺ�����ϵʽ��
��4������EFHG�ĶԽ���EH��FG�ཻ�ڵ�O�䣬��OO���ADʱ��t��ֵΪ����OO���ADʱ��t��ֵΪ ��
���𰸡�
��1��
�⣺������֪��AE=2t��0��t��4��
�ߡ�BAD=60�㣬��AFE=90�㣬
��sin��BAD= ![]() ��
��
��EF= ![]() t
t
��2��
�⣺��AE=2t����AEF=30�㣬
��AF=t��
��H��D�غ�ʱ��
��ʱFH=8��t��
��GE=8��t��
��EG��AD��
���EGA=30�㣬
���ı���ABCD�����Σ�
���BAC=30�㣬
���BAC=��EGA=30�㣬
��AE=EG��
��2t=8��t��
��t= ![]()
��3��
�⣺��0��t�� ![]() ʱ��
ʱ��
��ʱ����EFHG������ABCD�ص�����ͼ��Ϊ����EFHG��
���ɣ�2����֪��AE=EG=2t��
��S=EFEG= ![]() t2t=2
t2t=2 ![]() t2��
t2��
�� ![]() ��t��4ʱ����ͼ1��
��t��4ʱ����ͼ1��
��CD��HG���ڵ�I��
��ʱ����EFHG������ABCD�ص�����ͼ��Ϊ�����FEGID��
��AE=2t��
��AF=t��EF= ![]() t��
t��
��DF=8��t��
��AE=EG=FH=2t��
��DH=2t����8��t��=3t��8��
�ߡ�HDI=��BAD=60�㣬
��tan��HDI= ![]() ��
��
��HI= ![]() DH��
DH��
��S=EFEG�� ![]() DHHI=2
DHHI=2 ![]() t2��
t2�� ![]() ��3t��8��2=��
��3t��8��2=�� ![]() t2+24
t2+24 ![]() t��32
t��32 ![]()

��4��4��3
���������⣺��4����OO���ADʱ����ͼ2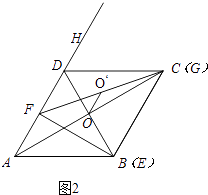
��ʱ��E��B�غϣ�
��t=4��
��OO���ADʱ����ͼ3��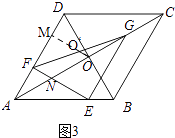
����O��OM��AD�ڵ�M��EF��OA�ཻ�ڵ�N��
�ɣ�2����֪��AF=t��AE=EG=2t��
��FN= ![]() t��
t��
��O���Ǿ���EFHG�ĶԽ��ߵĽ��㣬
��FM= ![]() EG=t��
EG=t��
��O��O��AD��O����FG���е㣬
��O��O�ǡ�FNG����λ�ߣ�
��O��O= ![]() FN=
FN= ![]() t��
t��
��AB=8��
���ɹ��ɶ�������ã�OA=4 ![]()
��OM=2 ![]() ��
��
��O��M=2 ![]() ��
�� ![]() t��
t��
��FE= ![]() t��EG=2t��
t��EG=2t��
���ɹ��ɶ�������ã�FG2=7t2 ��
���ɾ��ε����ʿ�֪��O��F2= ![]() FG2 ��
FG2 ��
���ɹ��ɶ�����֪��O��F2=O��M2+FM2 ��
�� ![]() t2=��2
t2=��2 ![]() ��
�� ![]() t��2+t2 ��
t��2+t2 ��
��t=3��t=��6����ȥ����
���Դ��ǣ�t=4��t=3��
�����㾫�����������ε����ʶ���Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪���ε������߶���ȣ����εĶԽ����ഹֱ������ÿһ���Խ���ƽ��һ��Խǣ����α������Խ��߷ֳ��ĸ�ȫ�ȵ�ֱ�������Σ����ε�������������Խ��߳��Ļ���һ�룮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ر������Ҳ���¶�t (��)��������������� h (km)�ı仯���仯��t��h ��һ����Χ�ڽ��Ƴ�һ�κ�����ϵ��
(1)�����±����� t(��)��h (km)֮��ĺ�����ϵʽ.
![]()
(2)���Ҳ��¶ȴﵽ 1770 ��ʱ���Ҳ����������Ϊ����ǧ�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�ٰ�һ��С�������ȣ���Ʒ�Ͻ�ʱ��Ϊ5��1����30�գ���ί���ͬѧ�ǽ�������Ʒ��ʱ��˳��ÿ5�����һ�飬��ÿһ��ļ�������ͳ�ƣ����Ƴ���ͼ��ʾ��ͳ��ͼ����֪�����Ҹ����εĸ߶ȱ�Ϊ2��3��4��6��4��1���������Ƶ����12�� 
����ش�
��1�����λ��������Ʒ������
��2������������ռ�ٷֱȻ��Ƴ�����ͳ��ͼ����ô�������Ӧ�����ε�Բ�Ľ����ȣ�
��3�����λ������2��һ�Ƚ���3�����Ƚ������Ƚ������㽱����������һ�����Ƚ���Ʒ���б�Ų������ɱ�����ȫһ�µĿ�Ƭ�����泯�ϵķ��ã����������ſ�Ƭ�����б�������״ͼ��鵽����Ʒǡ��һ����һ�Ƚ���һ���Ƕ��Ƚ��ĸ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����С����С�ա�Сӱһ���о�һ����ѧ�⣮��ͼ����֪EF��AB��CD��AB.
С��˵���������֪����CDG����BFE����ô�ܵõ���AGD����ACB.��
С��˵������С������֪�ͽ��۵����������ɡ�AGD����ACB���ɵõ���CDG����BFE.��
С��˵������AGDһ�����ڡ�BFE.��
Сӱ˵�����������GF����ôGFһ��ƽ����AB.��
���������У���________���˵�˵������ȷ�ģ�(����)

A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB��90������D��E�ֱ���AB��AC�ϣ�CE��BC������CD�����߶�CD�Ƶ�C��˳ʱ�뷽����ת90�����CF������EF.
(1)�������ͼ�Σ�
(2)��EF��CD����֤����BDC��90��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC �У�AB=AC=6cm����B=��C��BC=4cm���� D Ϊ AB���е㣮
��1������� P ���߶� BC ���� 1cm/s ���ٶ��ɵ� B ��� C �˶���ͬʱ���� Q ���߶� CA ���ɵ� C ��� A �˶���
������ Q ���˶��ٶ���� P ���˶��ٶ���ȣ����� 1 �����BPD ����CQP �Ƿ�ȫ�ȣ���˵�����ɣ�
������ Q ���˶��ٶ���� P ���˶��ٶȲ���ȣ����� Q ���˶��ٶ�Ϊ����ʱ���ܹ�ʹ��BPD ����CQP ȫ�ȣ�
��2������ Q �Ԣ��е��˶��ٶȴӵ� C �������� P ��ԭ�����˶��ٶȴӵ� B ͬʱ����������ʱ���ء�ABC �����˶����� �� P ��� Q ��һ���ڡ�ABC �� �������������ں�����ֱ��д���𰸣�������д������̣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
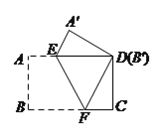
����Ŀ����һ�ų�����ֽƬ����ͼ��ʽ�۵���ʹ����![]() �͵�
�͵�![]() �غϣ��ۺ�Ϊ
�غϣ��ۺ�Ϊ![]() ����
����![]() ��
�� ![]() ��
��
��![]() ��
��![]() �ij���
�ij���
��![]() ���ص�����
���ص�����![]() �������
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵ�У����ǰѺᡢ�����궼Ϊ�����ĵ��Ϊ���㣬�Ƕ��㶼�������������Ϊ���������Σ���ͼ����֪����A��2��3����B��4��4���������������������߽磩�ϰ�Ҫ�����������Σ�
��1����ͼ1�л�һ����PAB��ʹ��P�ĺᡢ������֮�͵��ڵ�A�ĺ����ꣻ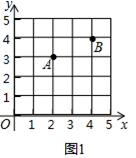
��2����ͼ2�л�һ����PAB��ʹ��P��B�������ƽ���͵�������������͵�4����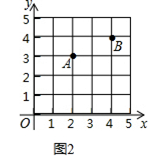
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��AB=CD��DE��AC��BF��AC��E��F�Ǵ��㣬DE=BF��
��֤����1��AF=CE��
��2��AB��CD��
��3��AD=CB��AD��CB��
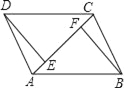
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com