
【题目】如图,在平面直角坐标系中,点O为坐标原点,抛物线![]() 交x轴负半轴于点A,交x轴正半轴于点B,交y轴负半轴于点C,
交x轴负半轴于点A,交x轴正半轴于点B,交y轴负半轴于点C,![]() ,
,![]() .
.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 点D在抛物线
点D在抛物线![]() 在第一象限的部分上,连接BC,DC,过点D作x轴的垂线,点E为垂足,
在第一象限的部分上,连接BC,DC,过点D作x轴的垂线,点E为垂足,![]() 的正切值等于
的正切值等于![]() 的正切值的一半,求点D的坐标;
的正切值的一半,求点D的坐标;
![]() 在
在![]() 的条件下,横坐标为t的点P在抛物线
的条件下,横坐标为t的点P在抛物线![]() 在第四象限的部分上,PB的延长线交DE于点F,连接BD,OF交于点G,连接EG,若GB平分
在第四象限的部分上,PB的延长线交DE于点F,连接BD,OF交于点G,连接EG,若GB平分![]() ,求t值.
,求t值.


【答案】(1)![]() ;(2)
;(2)![]() ;(3)t的值为2.
;(3)t的值为2.
【解析】
![]() 先确定
先确定![]() ,
,![]() ,然后利用待定系数法求抛物线解析式;
,然后利用待定系数法求抛物线解析式;
![]() 作
作![]() 于H,如图1,设
于H,如图1,设![]() ,再解方程
,再解方程![]() 得
得![]() ,利用正切的定义得到
,利用正切的定义得到![]() ,则
,则![]() ,然后解方程求出x即可得到D点坐标;
,然后解方程求出x即可得到D点坐标;
![]() 如图2,先利用待定系数法求出直线BD的解析式为
如图2,先利用待定系数法求出直线BD的解析式为![]() ,设
,设![]() ,再利用角平分线的性质定理得到GO:
,再利用角平分线的性质定理得到GO:![]() :BE,则
:BE,则![]() ,所以
,所以![]() ,解方程得到
,解方程得到![]() ,接着求出直线BD与OG的交点F的坐标为
,接着求出直线BD与OG的交点F的坐标为![]() ,然后利用待定系数法求出直线BF的解析式为
,然后利用待定系数法求出直线BF的解析式为![]() ,最后解方程组
,最后解方程组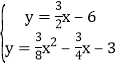 得t的值.
得t的值.
![]() ,
,![]() .
.
![]() ,
,![]() ,
,
把![]() ,
,![]() 代入
代入![]() 得
得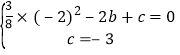 ,解得
,解得 ,
,
![]() 抛物线解析式为
抛物线解析式为![]() ;
;
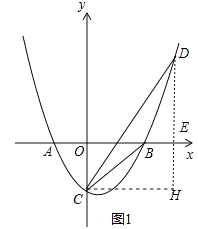
![]() 作
作![]() 于H,如图1,
于H,如图1,
设![]() ,
,
当![]() 时,
时,![]() ,解得
,解得![]() ,
,![]() ,则
,则![]() ,
,
在![]() 中,
中,![]() ,
,
![]() 的正切值等于
的正切值等于![]() 的正切值的一半
的正切值的一半
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,解得得
,解得得![]() ,
,![]() ,则
,则![]() ;
;
![]() 如图2,
如图2,

设直线BD的解析式为![]() ,
,
把![]() ,
,![]() 代入得
代入得![]() ,解得
,解得![]() ,
,
![]() 直线BD的解析式为
直线BD的解析式为![]() ,
,
设![]() ,
,
![]() 平分
平分![]() ,
,
![]() :
:![]() :BE,
:BE,
即GO:![]() :2,
:2,
![]() ,
,
![]() ,
,
整理得![]() ,解得
,解得![]() ,
,![]() ,
,
![]() ,
,
易得直线OF的解析式为![]() ,
,
当![]() 时,
时,![]() ,则
,则![]() ,
,
设直线BF的解析式为![]() ,
,
把![]() ,
,![]() 代入得
代入得![]() ,解得
,解得
![]() 直线BF的解析式为
直线BF的解析式为![]() ,
,
解方程组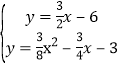 得
得![]() 或
或![]() ,
,
![]() ,
,
即t的值为2.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
【题目】为了帮助本市一名患“白血病”的高中生,某班15名同学积极捐款,他们捐款数额如下表:
捐款的数额(单位:元) | 5 | 10 | 20 | 50 | 100 |
人数(单位:个) | 2 | 4 | 5 | 3 | 1 |
关于这15名同学所捐款的数额,下列说法正确的是
A.众数是100 B.平均数是30 C.极差是20 D.中位数是20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】梧州市特产批发市场有龟苓膏粉批发,其中A品牌的批发价是每包20元,B品牌的批发价是每包25元,小王需购买A,B两种品牌的龟苓膏粉共1000包.
(1)若小王按需购买A,B两种品牌龟苓膏粉共用22000元,则各购买多少包?
(2)凭会员卡在此批发市场购买商品可以获得8折优惠,会员卡费用为500元.若小王购买会员卡并用此卡按需购买1000包龟苓膏粉,共用了y元,设A品牌买了x包,请求出y与x之间的函数关系式;
(3)在(2)中,小王共用了20000元,他计划在网店包邮销售这批龟苓膏粉,每包龟苓膏粉小王需支付邮费8元,若每包销售价格A品牌比B品牌少5元,请你帮他计算,A品牌的龟苓膏粉每包定价不低于多少元时才不亏本?(运算结果取整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
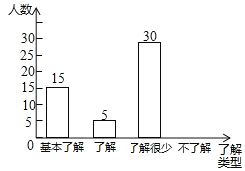
【题目】“校园安全”受到全社会的广泛关注,“高远”中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如下尚不完整的条形统计图,且知在抽样调查中“了解很少”的同学占抽样调查人数的![]() ,请你根据提供的信息解答下列问题:
,请你根据提供的信息解答下列问题:
![]() 接受问卷调查的学生共有多少名?
接受问卷调查的学生共有多少名?
![]() 请补全条形统计图;
请补全条形统计图;
![]() 若“高远”中学共有1800名学生,请你估计该校学生对校园知识“基本了解”的有多少名?
若“高远”中学共有1800名学生,请你估计该校学生对校园知识“基本了解”的有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
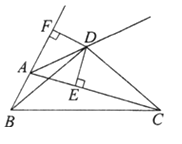
【题目】如图,D为∠BAC的外角平分线上一点,并且满足BD=CD,过D作DE⊥AC于E,DF⊥AB交BA的延长线于F,则下列结论:①![]() ;②∠DBC=∠DCB;③CE=AB+AE④∠BDC=∠BAC,其中正确的结论有( )
;②∠DBC=∠DCB;③CE=AB+AE④∠BDC=∠BAC,其中正确的结论有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习投影后,小明、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图所示,在同一时间,身高为1.6 m的小明(AB)的影子BC长是3m,而小颖(EH)刚好在路灯灯泡的正下方H点,并测得HB=6m.
(1)请在图中画出形成影子的光线,并确定路灯灯泡所在的位置G;
(2)求路灯灯泡的垂直高度GH;
(3)如果小明沿线段BH向小颖(点H)走去,当小明走到BH中点B1处时,求其影子B1C1的长;当小明继续走剩下的路程的![]() 到B2处时,求其影子B2C2的长;当小明继续走剩下路程的
到B2处时,求其影子B2C2的长;当小明继续走剩下路程的![]() 到B3处时,……按此规律继续走下去,当小明走剩下路程的
到B3处时,……按此规律继续走下去,当小明走剩下路程的![]() 到
到![]() 处时,其影子
处时,其影子![]() 的长为________m(直接用含n的代数式表示).
的长为________m(直接用含n的代数式表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:选取二次三项式![]() 中两项,配成完全平方式的过程叫配方,配方的基本形式是完全平方公式的逆写,即
中两项,配成完全平方式的过程叫配方,配方的基本形式是完全平方公式的逆写,即![]() .例如:
.例如:
①选取二次项和一次项配方:![]()
②选取二次项和常数项配方:![]() ,或
,或![]()
③选取一次项和常数项配方:![]()
请根据阅读材料解决下列问题:
(1)比照上面的例子,将二次三项式![]() 配成完全平方式(直接写出两种形式);
配成完全平方式(直接写出两种形式);
(2)将![]() 分解因式;
分解因式;
(3)已知![]() 、
、![]() 、
、![]() 是
是![]() 的三边长,且满足
的三边长,且满足![]() ,试判断此三角形的形状.
,试判断此三角形的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果∠A和∠B互补,且∠A>∠B,给出下列四个式子:①90°﹣∠B;②∠A﹣90°;③![]() ∠A+∠B;④
∠A+∠B;④![]() (∠A﹣∠B),其中表示∠B余角的式子有( )
(∠A﹣∠B),其中表示∠B余角的式子有( )
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一枚棋子放在边长为1个单位长度的正六边形

ABCDEF的顶点A处,通过摸球来确定该棋子的走法,其规则是:在
一只不透明的袋子中,装有3个标号分别为1、2、3的相同小球,搅匀
后从中任意摸出1个,记下标号后放回袋中并搅匀,再从中任意摸出1
个,摸出的两个小球标号之和是几棋子就沿边按顺时针方向走几个单位
长度.
棋子走到哪一点的可能性最大?求出棋子走到该点的概率.(用列表或画树状图的方法
求解)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com