
��ͼ����ƽ��ֱ������ϵ�У�����OABC�ı�OA=2��OC=6����OC��ȡ��D����AOD��AD���ۣ�ʹO������AB���ϵ�E�㴦����һ���㹻���ֱ�����ǰ�Ķ���P��D��������߶�DA��AB�ƶ�����һֱ�DZ�ʼ�վ�����D����һֱ�DZ�����ֱ����ֱ��DE��BC�ֱ��ڵ�M��N��
��1����գ�D�������ǣ���������������E�������ǣ���������������
��2����ͼ1������P���߶�DA���ƶ�ʱ���Ƿ���������ĵ�M��ʹ��CMNΪ���������Σ������ڣ������M�����ꣻ�������ڣ���˵�����ɣ�
��3����ͼ2������P���߶�AB���ƶ�ʱ����P������Ϊ��x��2�����ǡ�DBN�����ΪS����ֱ��д��S��x֮��ĺ�����ϵʽ�������S��x�������Сʱ����Ӧ���Ա���x��ȡֵ��Χ��
��1����2��0������2��2����
��2�����ڵ�Mʹ��CMNΪ���������Σ�M�������Ϊ����2��0������2��4������2��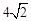 ��4����
��4����
��3��S��x�������Сʱ��0��x��2��4��x��6��
���������������1�����ݡ�AOD��AD���ۣ�ʹO������AB���ϵ�E�㴦���õ���OAD=��EAD=45�㣬DE=OD�����OD=2���ó�D������꣬�ٸ���DE=OD=2�����E������꣺
�߽���AOD��AD���ۣ�ʹO������AB���ϵ�E�㴦��
���OAD=��EAD=45�㣬DE=OD����OA=OD��
��OA=2����OD=2����D�������ǣ�2��0����DE=OD=2����E�������ǣ�2��2����
��2���ɷ��ۿ�֪�ı���AODEΪ�����Σ���M��MH��BC��H���������NMH=��MNH=45�㣬�ó�NH=MH=4��MN=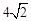 ���ٸ���ֱ��OE�Ľ���ʽΪ��y=x���������MN��OE����MN�Ľ���ʽΪy=x+b������DE�Ľ���ʽΪx=2��BC�Ľ���ʽΪx=6���ó�M��2��2+b����N��6��6+b����
���ٸ���ֱ��OE�Ľ���ʽΪ��y=x���������MN��OE����MN�Ľ���ʽΪy=x+b������DE�Ľ���ʽΪx=2��BC�Ľ���ʽΪx=6���ó�M��2��2+b����N��6��6+b����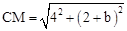 ��CN=6+b��MN=
��CN=6+b��MN=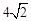 ����CM=CN��CM=MN�� CM=MN��������ֱ������M�����ꡣ
����CM=CN��CM=MN�� CM=MN��������ֱ������M�����ꡣ
��3������������֤����PBN�ס�DEP���ó�BN��ֵ�����S��x֮��ĺ�����ϵʽ����������ã�
��0��x��2ʱ��
�ߡ�BPN+��DPE=90�㣬��BPN+��EPD=90�㣬���DPE=��EPD��
���PBN�ס�DEP����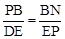 ����
����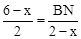 ����
����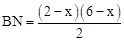 ��
��
��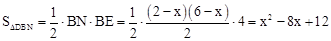 ��
��
��2��x��6ʱ��
�ߡ�PBN�ס�DEP����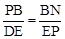 ����
����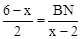 ����
���� ��
��
��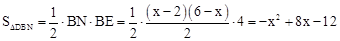 ��
��
��S��x֮��ĺ�����ϵʽ��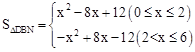 ��
��
���ݢٵ�0��x��2ʱ��S=x2��8x+12=��x��4��2��4���ڵ�2��x��6ʱ��S=��x2+8x��12=����x��4��2+4�����ɵó��𰸡�
�⣺��1����2��0������2��2����
��2�����ڵ�Mʹ��CMNΪ���������Σ��������£�
�ɷ��ۿ�֪�ı���AODEΪ�����Σ�
��M��MH��BC��H��
�ߡ�PDM=��PMD=45�㣬
���NMH=��MNH=45�㡣NH=MH=4��MN=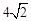 ��
��
��ֱ��OE�Ľ���ʽΪ��y=x���������MN��OE��
����MN�Ľ���ʽΪy=x+b��
��DE�Ľ���ʽΪx=2��BC�Ľ���ʽΪx=6����M��2��2+b����N��6��6+b����
��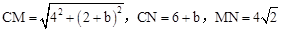 ��
��
������������ۣ�
�ٵ�CM=CNʱ��42+��2+b��2=��6+b��2����ã�b=��2��
��ʱM��2��0����
�ڵ�CM=MNʱ��42+��2+b��2=��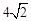 ��2����ã�b1=2��b1=��6������������ȥ����
��2����ã�b1=2��b1=��6������������ȥ����
��ʱM��2��4����
�۵�CM=MNʱ��6+b=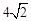 ����ã�b=
����ã�b=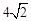 ��6��
��6��
��ʱM��2��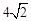 ��4����
��4����
�������������ڵ�Mʹ��CMNΪ���������Σ�M�������Ϊ��
��2��0������2��4������2��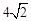 ��4����
��4����
��3��S��x֮��ĺ�����ϵʽΪ��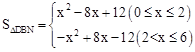 ��
��
�ٵ�0��x��2ʱ��S=x2��8x+12=��x��4��2��4��
��x��4ʱ��S��x���������С����0��x��2��
�ڵ�2��x��6ʱ��S=��x2+8x��12=����x��4��2+4��
��x��4ʱ��S��x���������С����4��x��6��
����������S��x�������Сʱ��0��x��2��4��x��6��


 ͨ��ѧ��Ĭд����ϵ�д�
ͨ��ѧ��Ĭд����ϵ�д� ���ƽ̸�������ѡ����ĩ���100��ϵ�д�
���ƽ̸�������ѡ����ĩ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����֪������y=ax2+bx+c��x���һ������A������Ϊ����1��0�����Գ���Ϊֱ��x=��2��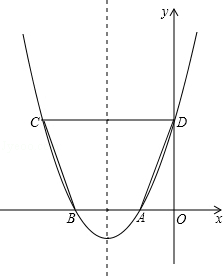
��1������������x�����һ������B�����ꣻ
��2����D����������y��Ľ��㣬��C���������ϵ���һ�㣮��֪��ABΪһ�ױߵ�����ABCD�����Ϊ9����������ߵĽ���ʽ����ָ������E�����ꣻ
��3����P�ǣ�2���������߶Գ�����һ���㣬����1����λ/����ٶȴӴ������ߵĶ���E�����˶������P�˶���ʱ��Ϊt�룮
�ٵ�tΪ�� ����ʱ����PAD���ܳ���С����tΪ�� ����ʱ����PAD����ADΪ���ĵ��������Σ�������������ţ�
�ڵ�P���˶������У��Ƿ����һ��P��ʹ��PAD����ADΪб�ߵ�ֱ�������Σ������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��2013��㶫÷��10�֣���ͼ����֪������y=2x2��2��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C��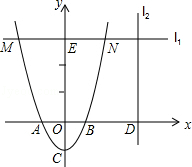
��1��д����A��B��CΪ����������������
��2������E��0��6������x��ƽ�е�ֱ��l1���������ཻ��M��N���㣨��M�ڵ�N����ࣩ����MNΪһ�ߣ��������ϵ���һ��PΪ��һ������ƽ���ı��Σ���ƽ���ı��ε����Ϊ8ʱ�������P�����ꣻ
��3������D��m��0��������m��1������x�ᴹֱ��ֱ��l2����һ��Q����Q�ڵ�һ���ޣ���ʹ����Q��D��BΪ����������κ���B��C��OΪ��������������ƣ����߶�QD�ij����ú�m�Ĵ���ʽ��ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����֪���κ���y=x2+bx+c����A��1��0����C��0����3��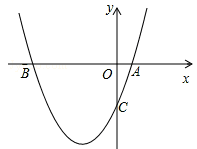
��1����˶��κ����Ľ���ʽ��
��2�����������ϴ���һ��Pʹ��ABP�����Ϊ10����ֱ��д����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����ƽ��ֱ������ϵxOy�У�ֱ��y=x+4��������ֱ���A��B���㣬��A��B�����������Ϊy=��x2+bx+c����DΪ�߶�AB��һ���㣬����D��CD��x���ڵ�C�����������ڵ�E��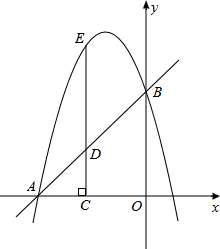
��1���������ߵĽ���ʽ��
��2����DE=4ʱ�����ı���CAEB�������
��3������BE���Ƿ���ڵ�D��ʹ�á�DBE�͡�DAC���ƣ������ڣ���˵�D���ꣻ�������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪����x�Ķ��κ���y=x2��2mx+m2+m��ͼ�������x�ĺ���y=kx+1��ͼ��������A��x1��y1����B��x2��y2������x1��x2��
��1����k=1��m=0��1ʱ����AB�ij���
��2����k=1��mΪ�κ�ֵʱ������AB�ij��Ƿ䣿��֤����IJ��룮
��3����m=0������kΪ��ֵʱ�������AOB����״��֤����IJ��룮
��ƽ���������ľ��빫ʽ ����
����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
ijУΪ����������Ƽ������������ٰ��˶����������С������˵���Բ���˶���һ�����Σ���ͼ��ʾ���ס�������ֱ��ֱ�������˵�A��B��˳ʱ�롢��ʱ��ķ���ͬʱ��Բ���˶������˶���·��l��cm����ʱ��t��s�������ϵ�� ��t��0��������4cm/s���ٶ������˶�����Բ�ij���Ϊ21cm��
��t��0��������4cm/s���ٶ������˶�����Բ�ij���Ϊ21cm��
��1�����˶�4s���·���Ƕ��٣�
��2���ס��Ҵӿ�ʼ�˶�����һ������ʱ�������˶��˶���ʱ�䣿
��3���ס��Ҵӿ�ʼ�˶����ڶ�������ʱ�������˶��˶���ʱ�䣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ1����֪������ABCD�ı߳�Ϊ1����E�ڱ�BC�ϣ�����AEF=900����EF����������ǵ�ƽ����CF�ڵ�F��
��1��ͼ1������E�DZ�BC���е㣬���ǿ��Թ�������������ȫ����֤��AE=EF�����������һ�����췽������ָ����������������ȫ�ȣ���Ҫ��֤������
��2����ͼ2������E���߶�BC�ϻ����������B��C�غϣ���
��AE=EF�Ƿ��ܳ����������֤����
������ͼ2��ֱ������ϵ�У�����E������ij��ʱ����Fǡ������������ �ϣ����ʱ��F�����꣮
�ϣ����ʱ��F�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ���ѡ��
����ͼ��MN��PQ,����Ϊ��O����A��C��ֱ��MN���˶�����B��D��ֱ��PQ���˶�.˳�������A��B��C��D��Χ���ı���ABCD�����ı���ABCD�����Ϊ6ʱ����AC��Ϊx��BD��Ϊy������ͼ�ܱ�ʾy��x��ϵ��ͼ���ǣ� ��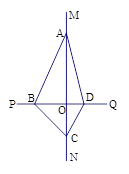
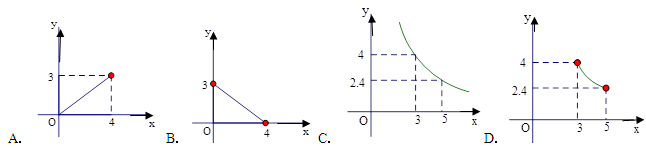
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com