
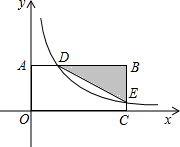
 如图,在平面直角坐标系中,BA⊥y轴于点A,BC⊥x轴于点C,函数y=$\frac{k}{x}$(x>0)的图象分别交BA,BC于点D,E,当AD:BD=1:4且△BDE的面积为3.6时,则k的值是2.25.
如图,在平面直角坐标系中,BA⊥y轴于点A,BC⊥x轴于点C,函数y=$\frac{k}{x}$(x>0)的图象分别交BA,BC于点D,E,当AD:BD=1:4且△BDE的面积为3.6时,则k的值是2.25. 分析 首先设B(5a,b),E(5a,d),利用AD:BD=1:4,则D(a,b),进而利用△BDE的面积为3.6得出ab-ad的值,结合反比例函数图象上的性质得出ab=5ad,进而得出ad的值,即可得出答案.
解答 解:如图,过点D作DF⊥x轴于点F,过点E作EG⊥y轴于点G.
设B(5a,b),E(5a,d).
∵AD:BD=1:4,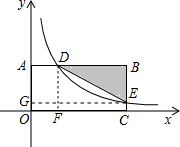
∴D(a,b).
又∵△BDE的面积为3.6,
∴BD=4a,BE=b-d,
∴$\frac{1}{2}$×4a(b-d)=3.6,
∴a(b-d)=1.8,即ab-ad=1.8,
∵D,E都在反比例函数图象上,
∴ab=5ad,
∴5ad-ad=1.8,
解得:ad=0.45,
∴k=5ad=2.25.
故答案为:2.25.
点评 此题主要考查了反比例函数综合应用以及三角形面积求法等知识,根据已知得出ab=5ad是解题关键.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:选择题
 如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(2,2),第2次接着运动到点(4,0),第3次接着运动到点(6,1),…,按这样的运动规律,经过第72次运动后,动点P的坐标是( )
如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(2,2),第2次接着运动到点(4,0),第3次接着运动到点(6,1),…,按这样的运动规律,经过第72次运动后,动点P的坐标是( )| A. | (144,0) | B. | (142,2) | C. | (72,0) | D. | (142,1) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,四边形ABCD是某公园里的长方形风景区,长AB=50m,宽BC=25m,为方便有人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1m,若小明沿着小路的中间,从出口A到出口B所走的路线(图中虚线)长为( )
如图,四边形ABCD是某公园里的长方形风景区,长AB=50m,宽BC=25m,为方便有人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1m,若小明沿着小路的中间,从出口A到出口B所走的路线(图中虚线)长为( )| A. | 100m | B. | 99m | C. | 98m | D. | 74m |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com