
【题目】二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A、B(5,0),与y轴交于点C,抛物线的顶点为M(2,-9),连接BM,点P为线段BM上的一个动点.
(1)求二次函数的解析式.
(2)过点P作x轴的垂线,垂足为点Q,求四边形ACPQ面积的最大值.
(3)是否存在点P,使得以P、M、C为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]() ,或
,或 ![]() 或
或![]()
【解析】
(1)根据抛物线的顶点为![]() ,将
,将![]() 化成顶点式
化成顶点式![]() ,然后将点
,然后将点![]() 代入,化简计算即可;
代入,化简计算即可;
(2)求出A,B,C三点的坐标,可得直线![]() 的表达式为
的表达式为![]() ,设点
,设点![]() ,则
,则![]() ,根据
,根据![]() 化简求解即可;
化简求解即可;
(3)分三种情况讨论:当![]() 时,当
时,当![]() 时,当
时,当![]() 时分别求解即可.
时分别求解即可.
解:(1)![]() 抛物线的顶点为
抛物线的顶点为![]() ,
,
![]() 设抛物线的表达式为
设抛物线的表达式为![]() .
.
将点![]() 代入得,
代入得,![]() .
.
解得![]()
![]() 二次函数的表达式为
二次函数的表达式为![]() ;
;
(2)令![]() ,得
,得![]() ,
,
![]()
![]() .
.
![]() 抛物线的对称轴为直线
抛物线的对称轴为直线![]() ,
,![]() ,
,
![]()
![]() .
.
由![]() ,
,![]() 可得直线
可得直线![]() 的表达式为
的表达式为![]() ,
,
设点![]() ,则
,则![]() ,
,
则![]()
![]() .
.
![]()
![]() ,
,![]() ,
,
![]() 当
当![]() 时,四边形
时,四边形![]() 面积有最大值,最大值为
面积有最大值,最大值为![]() ;
;
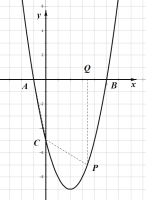
(3)存在,由(2)知直线![]() 的表达式为
的表达式为![]() .
.
设![]() ,其中
,其中![]() ,
,
由![]() ,
,![]() ,
,![]() 可得,
可得,
![]() ,
,![]() ,
,![]() ;
;
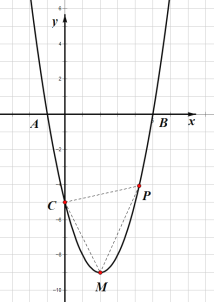
分情况讨论如下:
1. 当![]() 时,有
时,有![]() .
.
解得![]() (舍),
(舍),![]() ,
,
此时点![]() 的坐标为
的坐标为![]() ;
;
2. 当![]() 时,有
时,有![]() .
.
解得![]() (舍),
(舍),![]() ,
,
此时点![]() 的坐标为
的坐标为![]() ;
;
3. 当![]() 时,有
时,有![]() .
.
解得![]()
此时点![]() 的坐标为
的坐标为![]() ;
;
综上所述,当![]() 是等腰三角形时,点
是等腰三角形时,点![]() 的坐标为
的坐标为![]() ,或
,或 ![]() 或
或![]() .
.


 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
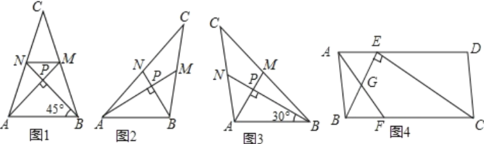
【题目】爱好思考的小明在探究两条直线的位置关系查阅资料时,发现了“中垂三角形”,即两条中线相互垂直的三角形“中垂三角形”,如图(1)、图(2)、图(3)中,AM、BN是△ABC的中线,AM⊥BN于点P,像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.
(特例研究)
(1)如图1,当tan∠PAB=1,c=4![]() 时,a=b= ;
时,a=b= ;
(归纳证明)
(2)请你观察(1)中的计算结果,猜想a2、b2、c2三者之间的关系,用等式表示出来,并利用图2证明你的结论;
(拓展证明)
(3)如图4,ABCD中,E、F分别是AD、BC的三等分点,且AD=3AE,BC=3BF,连接AF、BE、CE,且BE⊥CE于E,AF交BE相较于点G,AD=3![]() ,AB=3,求AF的长.
,AB=3,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=5cm,BD=8cm.点P从点B出发,沿BA方向匀速运动,速度为![]() ;同时,点Q从点D出发,沿DA方向匀速运动,速度为1cm/s.过点P作PN∥BC分别交BD,CD于点M,N,连接QM,QN.设运动时间为
;同时,点Q从点D出发,沿DA方向匀速运动,速度为1cm/s.过点P作PN∥BC分别交BD,CD于点M,N,连接QM,QN.设运动时间为![]() .解答下列问题:
.解答下列问题:
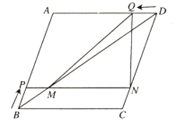
(1)当![]() 为何值时,点
为何值时,点![]() 在线段
在线段![]() 的垂直平分线上?
的垂直平分线上?
(2)设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)在运动过程中,是否存在某一时刻![]() ,使
,使![]() 的面积为菱形
的面积为菱形![]() 面积的
面积的![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(4)是否存在某一时刻![]() ,使
,使![]() 为等腰三角形?若存在,请直接写出
为等腰三角形?若存在,请直接写出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在宣传“民族团结”活动中,采用四种宣传形式:A.器乐,B.舞蹈,C.朗诵,D.唱歌.每名学生从中选择并且只能选择一种最喜欢的,学校就宣传形式对学生进行了抽样调查,并将调查结果绘制了如下两幅不完整的统计图.

请结合图中所给信息,解答下列问题:
(1)本次调查的学生共有_____人;
(2)补全条形统计图;
(3)该校共有1200名学生,请估计选择“唱歌”的学生有多少人?
(4)七年一班在最喜欢“器乐”的学生中,有甲、乙、丙、丁四位同学表现优秀,现从这四位同学中随机选出两名同学参加学校的器乐队,请用列表或画树状图法求被选取的两人恰好是甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
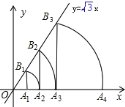
【题目】如图,直线![]() ,点A1坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按此做法进行下去,点A2020的坐标为______________.
,点A1坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按此做法进行下去,点A2020的坐标为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
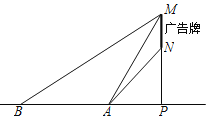
【题目】新冠肺炎疫情期间,小明同学想利用所学的知识测量他家对面某广告牌的宽度(图中线段MN的长),直线MN垂直于地面,垂足为点P.在地面A处测得点M的仰角为58°、点N的仰角为45°,在B处测得点M的仰角为30°,AB=5米,且A、B、P三点在一直线上.请根据以上数据求广告牌的宽MN的长.(参考数据:sin58°=0.85,cos58°=0.53,tan58°=1.60,![]() =1.73.)
=1.73.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生课外阅读情况,就学生每周阅读时间线上随机调查了部分学生,调查结果整理如下:
阅读时间人数统计表
阅读时间t(小时) | 人数 | 占人数百分比 |
0≤t<0.5 | 4 | 20% |
0.5≤t<1 | m | 15% |
1≤t<1.5 | 5 | 25% |
1.5≤t<2 | 6 | n |
2≤t<2.5 | 2 | 10% |
根据图表解答下列问题:
(1)此次抽样调查中,共抽取了 名学生;
(2)在阅读时间人数统计表中m= ,n= ;
(3)根据抽样调查的结果,请估计该校2000名学生中有多少名学生每天阅读时间在2≤t<2.5时间段?
查看答案和解析>>
科目:初中数学 来源: 题型:
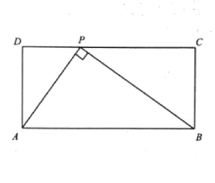
【题目】如图1,在矩形![]() 的边
的边![]() 上存在点
上存在点![]() ,使得
,使得![]() ,我们称点
,我们称点![]() 为矩形的“和谐点
为矩形的“和谐点
(1)求证: ![]() ;
;
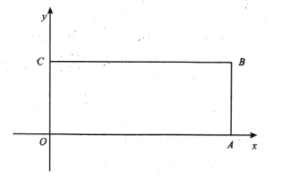
(2)如图2,矩形![]() 的顶点
的顶点![]() 的坐标为
的坐标为![]() 为坐标原点,点
为坐标原点,点![]() 分别在
分别在![]() 轴和
轴和![]() 轴上,在
轴上,在![]() 边上是否存在“和谐点”
边上是否存在“和谐点”![]() ,如果存在,求出点
,如果存在,求出点![]() 的坐标;如果不存在,请说明理由
的坐标;如果不存在,请说明理由
(3)在(2)中,如果点![]() 的坐标为
的坐标为![]() ,且在
,且在![]() 上存在“和谐点”
上存在“和谐点”![]() 求
求![]() 的取值范围
的取值范围
查看答案和解析>>
科目:初中数学 来源: 题型:
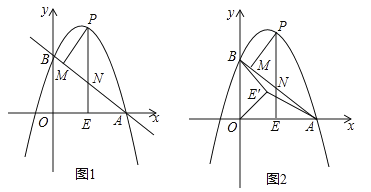
【题目】如图1,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,在
,在![]() 轴上有一动点
轴上有一动点![]() ,过点
,过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,交抛物线于点
,交抛物线于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .
.
(1)求![]() 的值和直线
的值和直线![]() 的函数表达式;
的函数表达式;
(2)设![]() 的周长为
的周长为![]() ,
,![]() 的周长为
的周长为![]() ,若
,若![]() ,求
,求![]() 的值;
的值;
(3)如图2,在(2)条件下,将线段![]() 绕点
绕点![]() 逆时针旋转得到
逆时针旋转得到![]() ,旋转角为
,旋转角为![]() ,连接
,连接![]() 、
、![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com