
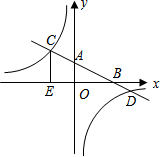
 如图,已知一次函数y=kx+b的图象分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,tan∠ABO=$\frac{1}{2}$,OB=4,OE=2.
如图,已知一次函数y=kx+b的图象分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,tan∠ABO=$\frac{1}{2}$,OB=4,OE=2.分析 (1)根据给定线段的长度以及∠ABO的正切值可求出点C的坐标,结合点C的坐标利用待定系数法即可求出反比例函数的解析式;
(2)结合B、C点的坐标利用待定系数法即可求出一次函数的解析式,将一次函数解析式代入到反比例函数解析式中得出关于x的一元二次方程,解方程即可求出D点的横坐标,将其代入反比例函数中即可求出D点的坐标,最后再由两点间的距离公式求出线段CD长度即可.
解答 解:(1)设该反比例函数的解析式为y=$\frac{m}{x}$,
∵tan∠ABO=$\frac{1}{2}$,OB=4,OE=2,
∴CE=$\frac{1}{2}$(OB+OE)=3,
∴点C的坐标为(-2,3).
∵点C在该反比例函数图象上,
∴3=$\frac{m}{-2}$,解得:m=-6.
∴该反比例函数的解析式为y=-$\frac{6}{x}$.
(2)∵点B(4,0),点C(-2,3)在一次函数y=kx+b的图象上,
∴有$\left\{\begin{array}{l}{0=4k+b}\\{3=-2k+b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=2}\end{array}\right.$.
∴一次函数的解析式为y=-$\frac{1}{2}$x+2.
令y=-$\frac{1}{2}$x+2=-$\frac{6}{x}$,即x2-4x-12=0,
解得:x=-2,或x=6.
∵当x=6时,y=-$\frac{6}{6}$=-1,
即点D的坐标为(6,-1).
∵点C坐标为(-2,3),
∴CD=$\sqrt{[6-(-2)]^{2}+(-1-3)^{2}}$=4$\sqrt{5}$.
点评 本题考查了反比例函数与一次函数的交点问题、待定系数法求函数解析式以及两点间的距离公式,解题的关键是:(1)求出点C的坐标;(2)求出点D的坐标.本题属于基础题,难度不大,解决该题型题目时,根据给定条件求出点的坐标,再结合点的坐标利用待定系数法求出函数解析式是关键.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | -1 | 0 | 0.5 | 2 |
| y | -1 | 2 | 3.75 | 2 |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
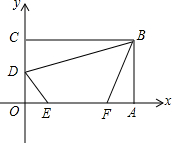 在平面直角坐标系中,矩形OABC如图所示.点A在x轴正半轴上,点C在y轴正半轴上,且OA=6,OC=4,D为OC中点,点E、F在线段OA上,点E在点F左侧,EF=2.当四边形BDEF的周长最小时,点E的坐标是( )
在平面直角坐标系中,矩形OABC如图所示.点A在x轴正半轴上,点C在y轴正半轴上,且OA=6,OC=4,D为OC中点,点E、F在线段OA上,点E在点F左侧,EF=2.当四边形BDEF的周长最小时,点E的坐标是( )| A. | ($\frac{1}{2}$,0) | B. | ($\frac{4}{3}$,0) | C. | ($\frac{3}{2}$,0) | D. | (2,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
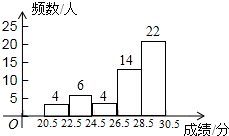 九年级(3)班共有50名同学,如图是该班一次体育模拟测试成绩的频数分布直方图(满分为30分,成绩均为整数).若将不低于23分的成绩评为合格,则该班此次成绩达到合格的同学占全班人数的百分比是( )
九年级(3)班共有50名同学,如图是该班一次体育模拟测试成绩的频数分布直方图(满分为30分,成绩均为整数).若将不低于23分的成绩评为合格,则该班此次成绩达到合格的同学占全班人数的百分比是( )| A. | 80% | B. | 70% | C. | 92% | D. | 86% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
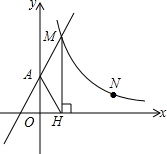 如图,直线y=2x+2与y轴交于A点,与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
如图,直线y=2x+2与y轴交于A点,与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系,A(a,0),B(b,0),C(-1,2),且|2a+b+1|+(a+2b-4)2=0.
如图,在平面直角坐标系,A(a,0),B(b,0),C(-1,2),且|2a+b+1|+(a+2b-4)2=0.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com