
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§OΈΣ‘≠ΒψΘ§ΤΫ––ΥΡ±Ώ–ΈABCDΒΡ±ΏBC‘Ύx÷α…œΘ§DΒψ‘Ύy÷α…œΘ§CΒψΉχ±ξΈΣΘ®2Θ§0Θ©Θ§BC=6Θ§ΓœBCD=60ΓψΘ§ΒψE «AB…œ“ΜΒψΘ§AE=3EBΘ§Γ―PΙΐDΘ§OΘ§C»ΐΒψΘ§≈ΉΈοœΏy=ax2+bx+cΙΐΒψDΘ§BΘ§C»ΐΒψΘ°
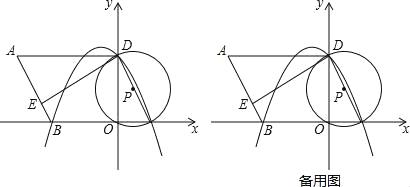
Θ®1Θ©«κ÷±Ϋ”–¥≥ωΒψBΓΔDΒΡΉχ±ξΘΚBΘ® Θ©Θ§DΘ® Θ©ΘΜ
Θ®2Θ©«σ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®3Θ©«σ÷ΛΘΚED «Γ―PΒΡ«–œΏΘΜ
Θ®4Θ©»τΒψMΈΣ≈ΉΈοœΏΒΡΕΞΒψΘ§«κ÷±Ϋ”–¥≥ωΤΫΟφ…œΒψNΒΡΉχ±ξΘ§ ΙΒΟ“‘ΒψBΘ§DΘ§MΘ§NΈΣΕΞΒψΒΡΥΡ±Ώ–ΈΈΣΤΫ––ΥΡ±Ώ–ΈΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©Θ®-4Θ§0Θ©ΘΜDΘ®0Θ§2![]() Θ©ΘΜΘ®2Θ©y=-
Θ©ΘΜΘ®2Θ©y=-![]() x2-
x2-![]() x+
x+![]() ΘΜ(3)÷ΛΟςΦϊΫβΈωΘΜΘ®4Θ©ΒψNΒΡΉχ±ξΈΣΘ®-5Θ§
ΘΜ(3)÷ΛΟςΦϊΫβΈωΘΜΘ®4Θ©ΒψNΒΡΉχ±ξΈΣΘ®-5Θ§![]() Θ©ΓΔΘ®3Θ§
Θ©ΓΔΘ®3Θ§![]() Θ©ΓΔΘ®-3Θ§-
Θ©ΓΔΘ®-3Θ§-![]() Θ©Θ°
Θ©Θ°
ΓΨΫβΈωΓΩ
‘ΧβΖ÷ΈωΘΚΘ®1Θ©œ»»ΖΕ®BΘ®-4Θ§0Θ©Θ§‘Ό‘ΎRtΓςOCD÷–άϊ”ΟΓœOCDΒΡ’ΐ«–«σ≥ωOD=2![]() Θ§Ω…ΒΟDΘ®0Θ§2
Θ§Ω…ΒΟDΘ®0Θ§2![]() Θ©ΘΜ
Θ©ΘΜ
Θ®2Θ©άϊ”ΟΫΜΒψ ΫΘ§¥ΐΕ®œΒ ΐΖ®Ω…«σ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®3Θ©œ»ΦΤΥψ≥ωCD=2OC=4Θ§‘ΌΗυΨίΤΫ––ΥΡ±Ώ–ΈΒΡ–‘÷ Θ§ΫαΚœœύΥΤ»ΐΫ«–ΈΒΡ≈–Ε®Ω…ΒΟΓςAEDΓΉΓςCODΘ§ΗυΨίœύΥΤ»ΐΫ«–ΈΒΡ–‘÷ ΚΆ‘≤÷ήΫ«Ε®άμΒΟΒΫCDΈΣΓ―PΒΡ÷±ΨΕΘ§”Ύ «ΗυΨί«–œΏΒΡ≈–Ε®Ε®άμΒΟΒΫED «Γ―PΒΡ«–œΏΘΜ
Θ®4Θ©άϊ”Ο≈δΖΫΒΟΒΫy=-![]() Θ®x+1Θ©2+
Θ®x+1Θ©2+![]() Θ§ΗυΨίΤΫ––ΥΡ±Ώ–ΈΒΡ–‘÷ ΚΆΒψΤΫ“ΤΒΡΙφ¬…Θ§άϊ”ΟΖ÷άύΧ÷¬έΒΡΖΫΖ®»ΖΕ®NΒψΉχ±ξΘ°
Θ§ΗυΨίΤΫ––ΥΡ±Ώ–ΈΒΡ–‘÷ ΚΆΒψΤΫ“ΤΒΡΙφ¬…Θ§άϊ”ΟΖ÷άύΧ÷¬έΒΡΖΫΖ®»ΖΕ®NΒψΉχ±ξΘ°
‘ΧβΫβΈωΘΚΘ®1Θ©ΓΏCΘ®2Θ§0Θ©Θ§BC=6Θ§
ΓύBΘ®-4Θ§0Θ©Θ§
‘ΎRtΓςOCD÷–Θ§ΓΏtanΓœOCD=![]() Θ§
Θ§
ΓύOD=2tan60Γψ=![]() Θ§
Θ§
ΓύDΘ®0Θ§![]() Θ©Θ°
Θ©Θ°
Θ®2Θ©…η≈ΉΈοœΏΒΡΫβΈω ΫΈΣy=aΘ®x+4Θ©Θ®x-2Θ©Θ§
Α―DΘ®0Θ§![]() Θ©¥ζ»κΒΟaΓΝ4ΓΝΘ®-2Θ©=
Θ©¥ζ»κΒΟaΓΝ4ΓΝΘ®-2Θ©=![]() Θ§ΫβΒΟa=-
Θ§ΫβΒΟa=-![]() Θ§
Θ§
Γύ≈ΉΈοœΏΒΡΫβΈω ΫΈΣy=-![]() Θ®x+4Θ©Θ®x-2Θ©=-
Θ®x+4Θ©Θ®x-2Θ©=-![]() x2-
x2-![]() x+
x+![]() ΘΜ
ΘΜ
Θ®3Θ©‘ΎRtΓςOCD÷–Θ§CD=2OC=4Θ§
ΓΏΥΡ±Ώ–ΈABCDΈΣΤΫ––ΥΡ±Ώ–ΈΘ§
ΓύAB=CD=4Θ§ABΓΈCDΘ§ΓœA=ΓœBCD=60ΓψΘ§AD=BC=6Θ§
ÿAE=3BEȧ
ΓύAE=3Θ§
Γύ![]() ,
,![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
ΓΏΓœDAE=ΓœDCBΘ§
ΓύΓςAEDΓΉΓςCODΘ§
ΓύΓœADE=ΓœCDOΘ§
ΓΏΓœADE+ΓœODE=90Γψ
ΓύΓœCDO+ΓœODE=90ΓψΘ§
ΓύCDΓΆDEΘ§
ΓΏΓœDOC=90ΓψΘ§
ΓύCDΈΣΓ―PΒΡ÷±ΨΕΘ§
ΓύED «Γ―PΒΡ«–œΏΘΜ
Θ®4Θ©¥φ‘ΎΘ°
ΓΏy=-![]() x2-
x2-![]() x+
x+![]() =-
=-![]() Θ®x+1Θ©2+
Θ®x+1Θ©2+![]() Θ§
Θ§
ΓύMΘ®-1Θ§![]() Θ©Θ§
Θ©Θ§
ΓΏBΘ®-4Θ§0Θ©Θ§DΘ®0Θ§![]() Θ©Θ§
Θ©Θ§
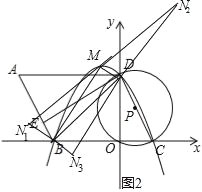
»γΆΦ2Θ§
Β±BMΈΣΤΫ––ΥΡ±Ώ–ΈBDMNΒΡΕ‘Ϋ«œΏ ±Θ§ΒψDœρΉσΤΫ“Τ4ΗωΒΞΈΜΘ§‘Όœρœ¬ΤΫ“Τ![]() ΗωΒΞΈΜΒΟΒΫΒψBΘ§‘ρΒψMΘ®-1Θ§
ΗωΒΞΈΜΒΟΒΫΒψBΘ§‘ρΒψMΘ®-1Θ§![]() Θ©œρΉσΤΫ“Τ4ΗωΒΞΈΜΘ§‘Όœρœ¬ΤΫ“Τ
Θ©œρΉσΤΫ“Τ4ΗωΒΞΈΜΘ§‘Όœρœ¬ΤΫ“Τ![]() ΗωΒΞΈΜΒΟΒΫΒψN1Θ®-5Θ§
ΗωΒΞΈΜΒΟΒΫΒψN1Θ®-5Θ§![]() Θ©ΘΜ
Θ©ΘΜ
Β±DMΈΣΤΫ––ΥΡ±Ώ–ΈBDMNΒΡΕ‘Ϋ«œΏ ±Θ§ΒψBœρ”“ΤΫ“Τ3ΗωΒΞΈΜΘ§‘Όœρ…œΤΫ“Τ![]() ΗωΒΞΈΜΒΟΒΫΒψMΘ§‘ρΒψDΘ®0Θ§
ΗωΒΞΈΜΒΟΒΫΒψMΘ§‘ρΒψDΘ®0Θ§![]() Θ©œρ”“ΤΫ“Τ3ΗωΒΞΈΜΘ§‘Όœρ…œΤΫ“Τ
Θ©œρ”“ΤΫ“Τ3ΗωΒΞΈΜΘ§‘Όœρ…œΤΫ“Τ![]() ΗωΒΞΈΜΒΟΒΫΒψN2Θ®3Θ§
ΗωΒΞΈΜΒΟΒΫΒψN2Θ®3Θ§![]() Θ©ΘΜ
Θ©ΘΜ
Β±BDΈΣΤΫ––ΥΡ±Ώ–ΈBDMNΒΡΕ‘Ϋ«œΏ ±Θ§ΒψMœρΉσΤΫ“Τ3ΗωΒΞΈΜΘ§‘Όœρœ¬ΤΫ“Τ![]() ΗωΒΞΈΜΒΟΒΫΒψBΘ§‘ρΒψDΘ®0Θ§
ΗωΒΞΈΜΒΟΒΫΒψBΘ§‘ρΒψDΘ®0Θ§![]() Θ©œρ”“ΤΫ“Τ3ΗωΒΞΈΜΘ§‘Όœρœ¬ΤΫ“Τ
Θ©œρ”“ΤΫ“Τ3ΗωΒΞΈΜΘ§‘Όœρœ¬ΤΫ“Τ![]() ΗωΒΞΈΜΒΟΒΫΒψN3Θ®-3Θ§-
ΗωΒΞΈΜΒΟΒΫΒψN3Θ®-3Θ§-![]() Θ©Θ§
Θ©Θ§
Ήέ…œΥυ ωΘ§ΒψNΒΡΉχ±ξΈΣΘ®-5Θ§![]() Θ©ΓΔΘ®3Θ§
Θ©ΓΔΘ®3Θ§![]() Θ©ΓΔΘ®-3Θ§-
Θ©ΓΔΘ®-3Θ§-![]() Θ©Θ°
Θ©Θ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ…η y=|x©¹1|+|x+1|Θ§‘ρœ¬ΟφΥΡΗωΫα¬έ÷–’ΐ»ΖΒΡ «Θ® Θ©
A. y ΟΜ”–Ήν–Γ÷Β B. ÷Μ”–“ΜΗω x Ι y »ΓΉν–Γ÷Β
C. ”–œόΗω xΘ®≤Μ÷Ι“ΜΗωΘ©y »ΓΉν–Γ÷Β D. ”–Έό«νΕύΗω x Ι y »ΓΉν–Γ÷Β
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘Ύœ¬Ν–ΗςΒψ÷–Θ§”κΒψAΘ®Θ≠2Θ§Θ≠4Θ©ΒΡΝ§œΏΤΫ––”ΎX÷αΒΡ «Θ® Θ©
A. Θ®2Θ§-4Θ© B. Θ®4Θ§-2Θ© C. Θ®-2Θ§4Θ© D. Θ®-4Θ§2Θ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣΓςABC÷–Θ§ΓœB=90ΓψΘ§AB=8cmΘ§BC=6cmΓΘ
Θ®1Θ©»τPΓΔQ «ΓςABC±Ώ…œΒΡΝΫΗωΕ·ΒψΘ§Τδ÷–ΒψP¥”A―ΊAΓζBΖΫœρ‘ΥΕ·Θ§ΥΌΕ»ΈΣΟΩΟκ1cmΘ§ΒψQ¥”B―ΊBΓζCΖΫœρ‘ΥΕ·Θ§ΥΌΕ»ΈΣΟΩΟκ2cmΘ§ΝΫΒψΆ§ ±≥ωΖΔΘ§…η≥ωΖΔ ±ΦδΈΣtΟκΘ°ΔΌΒ±t=1Οκ ±Θ§«σPQΒΡ≥ΛΘΜΔΎ¥”≥ωΖΔΦΗΟκ÷”ΚσΘ§ΓςPQB «Β»―ϋ»ΐΫ«–ΈΘΩ
Θ®2Θ©»τM‘ΎΓςABC±Ώ…œ―ΊBΓζAΓζCΖΫœρ“‘ΟΩΟκ3cmΒΡΥΌΕ»‘ΥΕ·Θ§‘ρΒ±ΒψM‘Ύ±ΏCA…œ‘ΥΕ· ±Θ§«σΓςBCM≥…ΈΣΒ»―ϋ»ΐΫ«–Έ ±M‘ΥΕ·ΒΡ ±ΦδΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»τa>bΘ§«“c<0Θ§‘ρac+1_____bc+1(ΧνΓΑ>Γ±ΜρΓΑ<Γ±).
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΎΕΰ¥ΈΚ· ΐy=Θ≠x2+2x+1ΒΡΆΦœσ÷–Θ§»τyΥφxΒΡ‘ω¥σΕχ‘ω¥σΘ§‘ρxΒΡ»Γ÷ΒΖΕΈß «Θ® Θ©
AΓΔx<1 BΓΔx>1 CΓΔx<Θ≠1 DΓΔx>Θ≠1
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
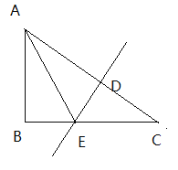
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ![]() ÷–Θ§
÷–Θ§![]() Θ§
Θ§![]() «
«![]() ΒΡ¥Ι÷±ΤΫΖ÷œΏΘ§ΫΜ
ΒΡ¥Ι÷±ΤΫΖ÷œΏΘ§ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ§ΫΜ
Θ§ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ°(1)ΓΔ»τΓœBAE=200Θ§«σ
Θ°(1)ΓΔ»τΓœBAE=200Θ§«σ![]() ΒΡΕ» ΐΓΘ(2)ΓΔ»τAB=6Θ§AC=10Θ§«σBEΒΡ≥ΛΓΘ
ΒΡΕ» ΐΓΘ(2)ΓΔ»τAB=6Θ§AC=10Θ§«σBEΒΡ≥ΛΓΘ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§L «“ΜΕΈΤΫ÷±ΒΡΧζΙλΘ§Ρ≥Χλ–ΓΟς’Ψ‘ΎΨύάκΧζΙλ100ΟΉΒΡA¥ΠΘ§ΥϊΖΔœ÷“ΜΝ–Μπ≥Β¥”Ήσœρ”“Ή‘‘ΕΖΫ Μά¥Θ§“―÷ΣΜπ≥Β≥Λ200ΟΉΘ§…ηΜπ≥ΒΒΡ≥ΒΆΖΈΣBΒψΘ§≥ΒΈ≤ΈΣCΒψΘ§–ΓΟς’ΨΉ≈≤ΜΕ·Θ§‘ρ¥”–ΓΟςΖΔœ÷Μπ≥ΒΒΫΜπ≥Β‘ΕάκΥϊΕχ»ΞΒΡΙΐ≥Χ÷–Θ§“‘AΓΔBΓΔC»ΐΒψΈΣΕΞΒψΒΡ»ΐΫ«–Έ «Β»―ϋ»ΐΫ«–ΈΒΡ ±ΩΧΙ≤”–Θ® Θ©

AΘ°2Ηω BΘ°3Ηω CΘ°4Ηω DΘ°5Ηω
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΎCCTVΓΑΩΣ–Ρ¥«ΒδΓ±άΗΡΩ÷–Θ§÷ς≥÷»ΥΈ ’β―υ“ΜΒάΧβΡΩΘΚΓΑa «Ήν–ΓΒΡ’ΐ’ϊ ΐΘ§b «Ήν¥σΒΡΗΚ’ϊ ΐΘ§c «ΨχΕ‘÷ΒΉν–ΓΒΡ”–άμ ΐΘ§«κΈ ΘΚaΘ§bΘ§c»ΐ ΐ÷°ΚΆ «__Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com